A) 3(2x + 3) - 5(7 – 4x) – 2(5x + 4)=-2
6х+9-35+20х-10х-8=-2
16х=-2-9+35+8
16х=32
х=2
6) 8(4 - 3x) + 7(x – 3) + 3(9 + 7x)= 10
32-24х+7х-21+27+21х=10
3х=10-32+21-27
4х=-28
х=-7
Объяснение:
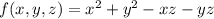
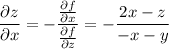
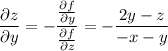
 с координатами
с координатами 
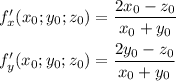
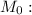
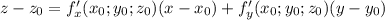 - уравнение касательной в общем виде.
- уравнение касательной в общем виде.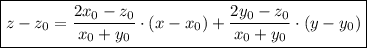 - уравнение касательной плоскости к поверхности в точке
- уравнение касательной плоскости к поверхности в точке  с координатами
с координатами 
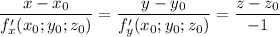
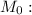
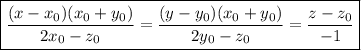 - каноническое уравнение нормали к поверхности в точке
- каноническое уравнение нормали к поверхности в точке  с координатами
с координатами 
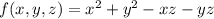
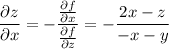
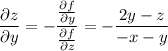
 с координатами
с координатами 
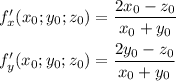
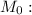
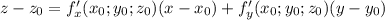 - уравнение касательной в общем виде.
- уравнение касательной в общем виде.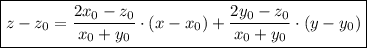 - уравнение касательной плоскости к поверхности в точке
- уравнение касательной плоскости к поверхности в точке  с координатами
с координатами 
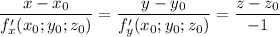
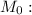
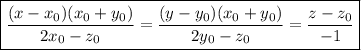 - каноническое уравнение нормали к поверхности в точке
- каноническое уравнение нормали к поверхности в точке  с координатами
с координатами 
Объяснение:
a) 3(2x + 3) - 5(7 – 4x) – 2(5x + 4)=-2
6х+9-35+20х-10х-8=-2
16х-34=-2
16х=-2+34
16х=32
х=2
б) 8(4 - 3x) + 7(x – 3) + 3(9 + 7x)= 10
32-24х+7х-21+27+21х=10
4х+38=10
4х=10-38
4х=-28
х=-7