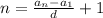
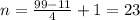
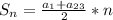
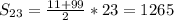
III. Формулювання мети і завдань уроку
Формулюємо проблему: як знайти значення виразу
.
де х1 і х2 – корені даного квадратного рівняння (не розв'язуючи рівняння)? Пошук відповіді на це запитання і вивчення сфери застосування теореми Вієта та теореми, оберненої до неї (вдосконалення вмінь), — основна мета уроку.
IV. Актуалізація опорних знань та вмінь
Виконання усних вправ
1. Замініть рівняння рівносильним йому зведеним квадратним рівняння:
а) 3х2 – 6х – 9 = 0; б) 2у2 + у – 7 = 0; в) х2 – 3х + 1,5 = 0
та знайдіть суму і добуток його коренів.
2. Наведіть приклад квадратного рівняння, в якого:
а) один корінь дорівнює нулю, а другий — не дорівнює нулю;
б) обидва корені дорівнюють нулю;
в) немає дійсних коренів;
г) корені — протилежні ірраціональні числа.
3. Один із коренів квадратного рівняння х2 + 4х – 21 = 0 дорівнює
sin(4α)
Объяснение:
1. Упростить выражение, используя формулу тригонометрических функций разницы углов:
sin (α – β) = sin α cos β – cos α sin β
получится:
sin(5α-α)
2. Приведём подобные члены, получится:
sin(4α)
ответ: sin(4α)