Числа при делении на 9 могут давать остатки 0,1,2,3,4,5,6,7,8,9. поєтому любое натуральное число можно записать в виде
n=9m+r, где m - некоторое неотрицательное число, r - цифра
Используя формулу куба суммы
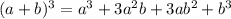
видим, что остаток от деления числа n^3 такой же как у числа b^3, так как
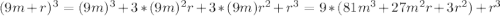
Рассмотрим остатки от деления кубов одноцифровых чисел
Кубы одноцифровых чисел 0, 1, 8, 27, 64, 125, 216, 343, 512, 729.
Числа 0, 27, 216, 729 при делении нацело на 9 дают остаток 0
Числа 1, 64, 343 при делении нацело на 9 дают в остатке 1
Числа 8, 125, 512 при делении нацело на 9 дают в остатке 8.
Таким образом делаем вывод, что кубы натуральных чисел при делении на 9 могут давать только остатка 0,1 и 8.
Доказано
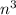 , по условию
, по условию 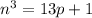 . Перенесём единицу в левую часть и разложим разность кубов на множители:
. Перенесём единицу в левую часть и разложим разность кубов на множители:
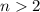 , тогда обе скобки-сомножителя - натуральные числа, большие 1. С другой стороны, произведение
, тогда обе скобки-сомножителя - натуральные числа, большие 1. С другой стороны, произведение 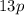 представляется в виде двух натуральных сомножителей, больших единицы, единственным (с точностью до перестановок
представляется в виде двух натуральных сомножителей, больших единицы, единственным (с точностью до перестановок 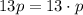 . Поэтому
. Поэтому  ,
,  равны либо
равны либо 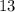 и
и 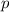 , либо
, либо 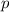 и
и 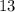 .
.
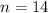 , тогда после подстановки во второе уравнение находим
, тогда после подстановки во второе уравнение находим 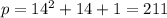 .
.  - действительно простое число, так что
- действительно простое число, так что 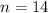 нас устраивает.
нас устраивает.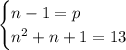
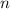 квадратное, а не линейное, как в первом случае. Упростив, получаем уравнение
квадратное, а не линейное, как в первом случае. Упростив, получаем уравнение 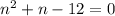 , у которого только один натуральный корень
, у которого только один натуральный корень 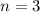 .
. - простое число, так что и тут нас всё устраивает.
- простое число, так что и тут нас всё устраивает. ,
, 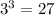
Надеюсь я тебе