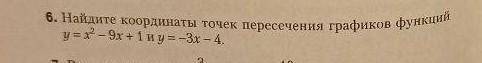
Алгебра: Кто решил можете .( только не методом Виета.)

Обозначим площадь грани кубика за а. Пусть в ряду имеется х кубиков. Тогда, у крайнего левого и крайнего правого в площади поверхности учитываются 5 сторон, у остальных - 4 стороны. Находим площадь поверхности: для крайних двух кубиков: для остальных (х-2) кубиков: общая: Пусть после добавления кубиков их устало у штук. Общая площадь поверхности в этом случае будет равна . По условию она увеличилась в k раз. Получаем равенство: Как видно и выражение и выражение при делении на 4 дает остаток...

Кто решил можете .( только не методом Виета.)

👇

Увидеть ответ

Ответ:

vika737722

30.06.2022

4,4

Объяснение:

4,5(16 оценок)

Ответ:

yuliaivanova1

30.06.2022

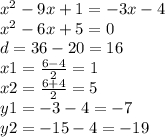
${x}^{2} - 9x + 1 = - 3x - 4 \\ {x}^{2} - 6x + 5 = 0 \\ d = 36 - 20 = 16 \\ x1 = \frac{6 - 4}{2} = 1 \\ x2 = \frac{6 + 4}{2} = 5 \\ y1 = - 3 - 4 = - 7 \\ y2 = - 15 - 4 = - 19$

(1;-7) (5;-19)

4,4(71 оценок)

Открыть все ответы

Ответ:

pashkevich00

30.06.2022

Два натуральных числа 16; 24.

Объяснение:

Найти два натуральных числа по заданным условиям.

Пусть первое число равно x, а второе равно y.

Тогда сумма их квадратов: x² + y² = 832,

а их произведение xy = 384.

Чтобы найти эти числа, решим систему уравнений.

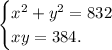
$\displaystyle \begin{cases} x^2 + y^2 = 832 \\ xy=384 . \end{cases}$

Умножим обе части второго уравнения системы на 2.

$\displaystyle \begin{cases} x^2 + y^2 = 832 \\ xy=384 \;\;|\cdot 2 \end{cases}; \;\;\; \; \displaystyle \begin{cases} x^2 + y^2 = 832 \\ 2xy=768 \end{cases}$

Сложим оба уравнения системы:

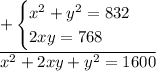
$\displaystyle +\begin{cases}x^2 + y^2 = 832\\2xy=768 \end{cases} \\\displaystyle \overline{x^2 +2xy+ y^2 = 1600}$

Свернем левую часть уравнения по формуле квадрата суммы двух выражений:

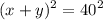
$\displaystyle (x+y)^2 = 40^{2}$

Получим следующую систему уравнений:

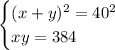
$\displaystyle \begin{cases} (x+y)^2 = 40^{2} \\ xy=384 \end{cases}$

Извлечем квадратный корень из обеих частей первого уравнения.

С учетом того, что нам даны натуральные числа, получим следующую систему уравнений:

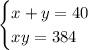
$\displaystyle \begin{cases} x+y = 40 \\ xy=384 \end{cases}$

Выразим переменную y через x в первом уравнении и подставим полученное выражение во второе уравнение.

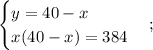
$\displaystyle \begin{cases} y = 40 -x\\ x(40-x)=384 \end{cases};$

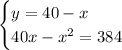
$\displaystyle \begin{cases} y = 40 -x\\ 40x -x^2=384 \end{cases}$

Решим второе уравнение системы.

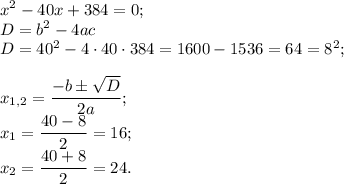
$\displaystyle x^2 -40x +384 = 0;\\\displaystyle D = b^{2} - 4ac \\D= 40^{2} -4\cdot 40 \cdot 384 =1600-1536=64=8^2;\\\\\displaystyle x_{1,2} =\frac{-b\pm\sqrt{D} }{2a};\\\displaystyle x_{1} =\frac{40-8}{2}=16;\\\displaystyle x_{2} =\frac{40+8}{2}=24.$

Тогда

$\displaystyle \begin{cases} x_{1}=16\\y_{1} = 40-16 \end{cases};\;\;\;\displaystyle \begin{cases} x_{1}=16\\y_{1} = 24 \end{cases};\\\\\displaystyle \begin{cases} x_{2}=24\\y_{2} = 40-24 \end{cases};\;\;\;\displaystyle \begin{cases} x_{2}=24\\y_{2}=16 \end{cases}$

Заданные натуральные числа 16 и 24.

4,7(79 оценок)

Ответ:

rudaniladanilov

30.06.2022

Обозначим площадь грани кубика за а.
Пусть в ряду имеется х кубиков. Тогда, у крайнего левого и крайнего правого в площади поверхности учитываются 5 сторон, у остальных - 4 стороны. Находим площадь поверхности:
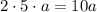
для крайних двух кубиков: $2\cdot5\cdot a=10a$
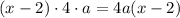
для остальных (х-2) кубиков: $(x-2)\cdot4\cdot a=4a(x-2)$
общая: 10a+4a(x-2)=10a+4ax-8a=4ax+2a=(4x+2)a

Пусть после добавления кубиков их устало у штук. Общая площадь поверхности в этом случае будет равна (4y+2)a

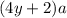. По условию она увеличилась в k раз. Получаем равенство: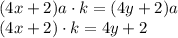
$(4x+2)a\cdot k=(4y+2)a \\\ (4x+2)\cdot k=4y+2$
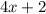Как видно и выражение 4x+2

и выражение 4y+2

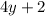при делении на 4 дает остаток 2. Однако при четном k=2n

возникает противоречие:
$(4x+2)\cdot 2n=4y+2 \\\ 4(2x+1)\cdot n=4y+2$
- левая часть кратна 4, в то время как правая по-прежнему при делении на 4 дает остаток 2. Значит k не может быть четным числом, и значение 6 недопустимо.
ответ: 6

4,4(21 оценок)

Это интересно:

Здоровье

23.01.2022

Симуляция головной боли: как это возможно и зачем это нужно?...

Компьютеры-и-электроника

24.04.2023

10 простых способов, как достать сияющего покемона...

Компьютеры-и-электроника

29.05.2022

Как подключить телевизор Samsung к беспроводной сети:...

Философия-и-религия