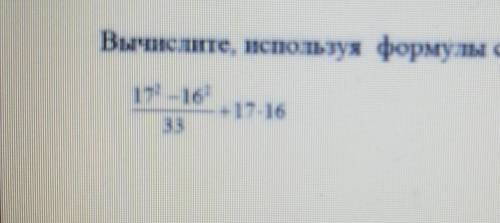
Запишем матрицу в виде:
1 2 -2
-2 -1 1
1 -2 1
Главный определитель
∆=1*((-1)*1 - (-2)*1) - (-2)*(2*1 - (-2)*(-2)) + 1*(2*1 - (-1)*(-2)) = -3
Определитель отличен от нуля, следовательно, матрица является невырожденной и для нее можно найти обратную матрицу A-1.
Обратная матрица будет иметь следующий вид:
A11 A21 A31
A12 A22 A32
A13 A23 A33
где Aij - алгебраические дополнения.
Транспонированная матрица.
AT=
1 -2 1
2 -1 -2
-2 1 1
Найдем алгебраические дополнения матрицы AT.
A1,1 = (-1)1+1
-1 -2
1 1
∆1,1 = ((-1)*1 - 1*(-2)) = 1
A1,2 = (-1)1+2
2 -2
-2 1
∆1,2 = -(2*1 - (-2)*(-2)) = 2
A1,3 = (-1)1+3
2 -1
-2 1
∆1,3 = (2*1 - (-2)*(-1)) = 0
A2,1 = (-1)2+1
-2 1
1 1
∆2,1 = -((-2)*1 - 1*1) = 3
A2,2 = (-1)2+2
1 1
-2 1
∆2,2 = (1*1 - (-2)*1) = 3
A2,3 = (-1)2+3
1 -2
-2 1
∆2,3 = -(1*1 - (-2)*(-2)) = 3
A3,1 = (-1)3+1
-2 1
-1 -2
∆3,1 = ((-2)*(-2) - (-1)*1) = 5
A3,2 = (-1)3+2
1 1
2 -2
∆3,2 = -(1*(-2) - 2*1) = 4
A3,3 = (-1)3+3
1 -2
2 -1
∆3,3 = (1*(-1) - 2*(-2)) = 3
Обратная матрица:
1 2 0
=1/-3 3 3 3
5 4 3
A-1=
-1/3 -2/3 0
-1 -1 -1
-5/3 -4/3 -1.
Проверим правильность нахождения обратной матрицы путем умножения исходной матрицы на обратную. Должны получить единичную матрицу E.
E=A*A-1=
1 2 -2
-2 -1 1
1 -2 1
1 2 0
1/-3 3 3 3
5 4 3
E=A*A-1=
1*1+2*3+(-2)*5 1*2+2*3+(-2)*4 1*0+2*3+(-2)*3
(-2)*1+(-1)*3+1*5 (-2)*2+(-1)*3+1*4 (-2)*0+(-1)*3+1*3
1*1+(-2)*3+1*5 1*2+(-2)*3+1*4 1*0+(-2)*3+1*3 =
-3 0 0
= 1/-3 0 -3 0
0 0 -3
A*A-1=
1 0 0
0 1 0
0 0 1.
Решение верно.

(17-16)×(17+16) делить на 33 +272=1×33 делить на 33+ +272= 33/33+272=1+272=273