Дано: (+3) + ( 2-5) Пайдите: а) степень многочлена; b) старший коэффициент и свободный член, с) сумму коэффициентов многочлена, d) сумму коэффициентов при четных степенях.
Рассмотрим две функции: и . Обе эти функции возрастающие. Тогда и функция, представляющая сумму эти[ функций, то есть функция будет возрастающей.
Таким образом, в левой части стоит возрастающая функция. Но возрастающая функция принимает каждое свое значение в единственной точке. Это означает, что если найден некоторый корень заданного уравнения, то других корней у уравнения нет.
Корень угадывается достаточно легко: . Проверка:
ответ: -1
б)
Аналогично, каждая из функций и возрастает. Значит, возрастает и функция .
Таким образом, уравнение имеет не более одного корня. Этот корень также легко подбирается: . Проверка:
Х мин. затрачивает отличник на решение одного примера (х+2,5) мин. затрачивает хорошист на решение одного примера 30/х примеров решит отличник за полчаса 30/(х+2,5) примеров решит хорошист за полчаса
Остаётся один корень х=5, это означает, что 5 мин. затрачивает отличник на решение одного примера. 4ч = 240 мин 240 мин. : 5 мин. = 48 примеров решит отличник за 4 часа. ответ: 48
а)
Рассмотрим две функции: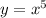
и 
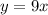. Обе эти функции возрастающие. Тогда и функция, представляющая сумму эти[ функций, то есть функция 
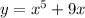будет возрастающей.
Таким образом, в левой части стоит возрастающая функция. Но возрастающая функция принимает каждое свое значение в единственной точке. Это означает, что если найден некоторый корень заданного уравнения, то других корней у уравнения нет.
Корень угадывается достаточно легко: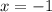
. Проверка:
ответ: -1
б)
Аналогично, каждая из функци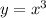й
и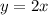 
возрастает. Значит, возрастает и функция 
.
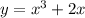Таким образом, уравнение имеет не более одного корня. Этот корень также легко подбирается: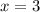
. Проверка:
ответ: 3