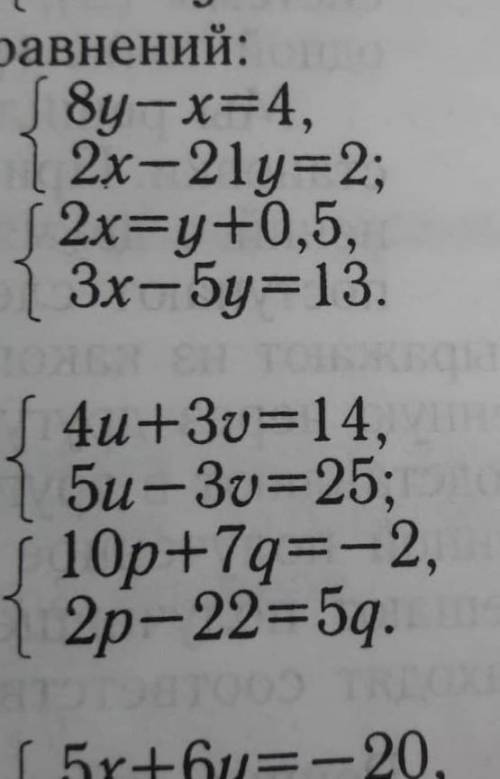
Постройте график функции y= x^2 - 4x + 4 найти область значения функции
y= x² - 4x + 4 ;
y = (x -2)²
График этой функции парабола , получается из графики функции у =x² перемещением по положительному направлению оси абсцисс _Ox
( направо) на две единицы . Вершина параболы оказывается в точке
на оси абсцисс с координатой x =2 * * * точка B(0 ; 2)_точка миним. * * *
ветви направленные вверх (по "+ 0у" ) .
График ось ординат пересекает в точке (0 ; 4) * * *x =0 ⇒y =(0 -2)² =4.* * *
y=(x -2)² ≥0
Минимальное значение функции равно нулю : Minу =0 , если x =2 .
Максимальное значение не имеетю
Область значения функции : E(y) = [ 0 ; +∞)
х = -20
у = -2
Объяснение:
Первая система
Выразим х
х = 8у - 4
Подставим во второе
2*(8у-4) - 21у = 2
16у - 8 - 21у = 2
-5у = 10
у = -2
Вернёмся к 1 уравнению
8*(-2) - х = 4
-16 - х = 4
х = -20