1) Б. С(3; 0; 0)
2. AO = √(x² + y² + z²) = √(9 + 1 + 25) = √35
3. a(-8; 4; -1), b(2; 3; -6)
1) |a| = √(64 + 16 + 1) = √81 = 9 (A)
2) |b| = √(4 + 9 + 36) = √49 = 7 (Б)
3) |a - b| = |(-10; 1; 5)| = √(100 + 1 + 25) = √126 = 3√14 (Д)
4) a·b = -8·2 + 4·3 + (-1)·(-6) = -16 + 12 + 6 = 2 (В)
4. x₁ = 2x₀ - x₂ = 8 + 2 = 10;
y₁ = 2y₀ - y₂ = -12 - 1 = -13;
z₁ = 2z₀ - z₂ = 22 - 7 = 15
A(10; -13; 15)
5. a·b = 0;
5·7 + n·4 - 3·9 = 0;
35 + 4n - 27 = 0;
4n = -8;
n = -2.
6. A(5; 8; 0), B(-7; 10; 2), C(3; 2; -3)
x₀ = (x₁ + x₂)/2 = (5 - 7)/2 = -2/2 = -1
y₀ = (y₁ + y₂)/2 = (8 + 10)/2 = 18/2 = 9
z₀ = (z₁ + z₂)/2 = (0 + 2)/2 = 2/2 = 1
E(-1; 9; 1)
CE = √(4² + 7² + 4²) = √(16 + 49 + 16) = √81 = 9
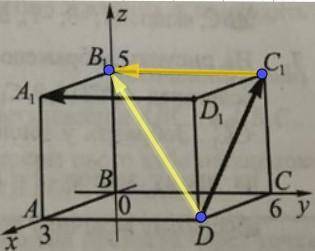
7. k = DB₁
DB₁ = √(a² + b² + c²) = √(BC² + BA² + BB₁²) = √(36 + 9 + 25) = √70
См. Объяснение
Объяснение:
№ 1
Задание
В прямоугольном треугольнике tgα=4. Найдите: sinα, cosα, ctgα.
Решение
1) tg²α = 1/cos²α - 1
4² = 1/cos²α - 1
1/cos²α - 1 = 16
(1-cos²α)/cos²α =16
16cos²α = 1-cos²α
17cos²α = 1
cos²α = 1/17
cosα = √(1/17) = √17/17 ≈ 0,2425356
2) tgα = sinα/cosα
sinα/cosα = 4
sinα/√17/17= 4
sinα = 4 · √17/17 = (4√17)/17 ≈ 0,9701425
3) ctg α = 1/tgα = 1/4 = 0,25
sinα = 4√17)/17 ≈ 0,9701425;
cosα = √17/17 ≈ 0,2425356;
ctgα = 0,25.
№ 2
Вычислить:
ctg240° + tg300° - sin(-225°) - cos495°.
Решение
1) ctg240° = ctg (180°+60°) = ctg60° = √3/3
2) tg300° = tg(270°+ 30°) = - сtg30° = - √3
3) - sin(-225°) = sin(225°) = sin(180° + 45°) = - sin45° = - √2/2
4) - cos 495° = - cos (360° + 135°) = - cos (135°) = - cos (180°- 45°) = cos 45° = √2/2
ctg240° + tg300° - sin(-225°) - cos495° = √3/3 - √3 - 2/2 +√2/2 =
= √3/3 - √3 ≈ - 1,1547
ответ: √3/3 - √3 ≈ - 1,1547