Сначала применим к выражению cos2x формулу косинуса двойного аргумента(1 её вариант). Затем получим уравнение, сводимое к алгебраическому. Получим:
2cos²x - 1 + 5cos x + 3 = 0
2cos²x + 5cos x + 2 = 0
Введём замену. Пусть cos x = t, причём |t| ≤ 1
Тогда получим обычкновенное квадратное уравнение:
2t² + 5t + 2 = 0
D = 25 - 16 = 9
t1 = (-5 - 3) / 4 = -8/4 = -2 - данный корень не удовлетворяет уравнению, поскольку мы наложили условие, что |t| ≤ 1
t2 = (-5+3) / 4 = -2/4 = -1/2 - подходит
cos x = -1/2
x = (-1)^k * arcsin(-1/2) + πk, k∈Z
x = (-1)^k+1 * π/6 + πk, k∈Z
ответ: (-1)^k+1 * π/6 + πk, k∈Z
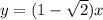
Графиком этой функции является прямая, проходящая через начало координат.
То, в каких четвертях она расположена зависит от того положителен или отрицателен коэффициент, стоящий при х. Если коэффициент больше нуля, то график расположен в первой и третьей четвертях. Если коэффициент меньше нуля, то график расположен во второй и четвёртой четвертях.
При х находится коэффициеннт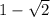 
.
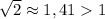, значит 
.
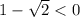Значит, график расположен во второй и четвёртой четвертях.
Аналогично рассмотрим второй пример уже без таких подробных разъяснений:
,
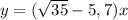
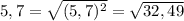значит
Следовательно, график 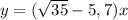расположен в первой и третьей четвертях.
y=3х-5 при х=-2
у=3•(-2)-5
у=11
при х=1,5
у=3•1,5-5
у=-0,5
при х=0
у=3•0-5
у=-5
при х=3
у=3•3-5
у=4
при у=-10
у=3•(-10)-5
у=-35