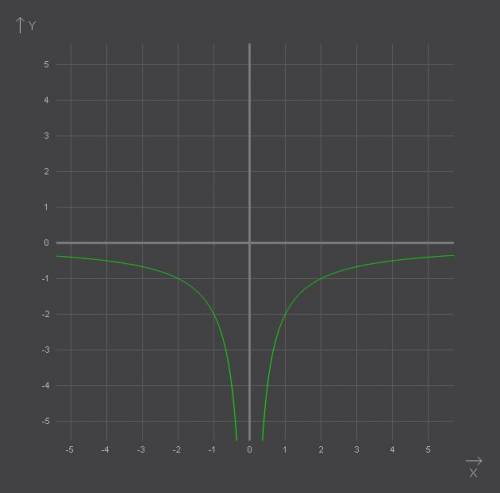
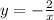представляет собой стандартную гиперболу 
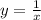, растянутую в 2 раза от оси абсцисс и отображенную симметрично относительно оси абсцисс. 
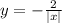нужно часть графика 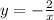, расположенную в левой полуплоскости, стереть, и отобразить в эту полуплоскость симметрично оси ординат часть графика, расположенную в правой полуплоскости.
Теперь краткая теория. Что подразумевается под "производной".
Определение значит звучит так:
f'(x)=
Где дельтой обозначены т.н. "приращения" аргумента и функции соответственно.
Приращение - некоторый промежуток, который мы получаем, если возьмем две точки x и x(0), вот разница x-x(0) (ну или x(0)-x) есть приращение аргумента.
Приращение функции, в свою очередь, есть y-y(0).
Такие приращения также заменяют бесконечно малыми приращениями и выглядит это уже без предела (беспредельщина)
Это и есть производная.
Свойств у нее несколько, мы будем использовать два:
(f+g)'=f'+g' и
Ну и нужна табличка производных. Из нее берем формулу для полиномиальной (или степенной) функции:
Тогда
Такие делы.
Получаем на нашем примере:
Осталось лишь раскрыть скобки и получить следующий ответ: