Четыре последовательных натуральных числа таковы , что произведение двух меньших из них чисел на 78 меньше ,чем произведение больших чисел. Найдите наименьшее из этих чисел.
Решение.
Пусть х - первое число, оно же является наименьшим;
(х+1) - второе число;
(х+2) - третье число;
(х+3) - четвертое число, тогда
х·(х+1) - это произведение двух меньших из данных чисел, а
(х+2)·(х+3) - это произведение двух больших из данных чисел.
По условию
х·(х+1) < (х+2)·(х+3) на 78
получаем уравнение:
(х+2)·(х+3) = х·(х+1) + 78 (ОДЗ; x∈N;)
x²+2x+3x+6 = x²+x+78
4x = 72
x = 72 : 4
x = 18
Получим четыре числа: 18; 19; 20; 21 из них
18 - является наименьшим.
ответ: 18.
1) Допустим, было
граммов 5%-ой кислоты. Тогда, очевидно, 10%-ой было 
.
Составляем уравнение:
5% ·
+ 10% ·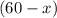 
= 8% · 60;
Тогда 5%-ого раствора было 24 г, а 10% - 60 - 24 = 36 (г).
ОТВЕТ: 5%-ого - 24 г, 10%-ого - 36 г.
2) Допусти, у нас есть
"десятирублевок". Тогда "пятирублевок" всего 
.
Составляем уравнение:
Десятирублевых монет - 7. Пятирублевых - 25 - 7 = 18
ОТВЕТ: десятирублевых - 7; пятирублевых - 18.
3) Пусть вагон весит
т. Тогда электровоз стоит 
.
Составляем уравнение:
Один вагон весит 16,8 т. Тогда электровоз весит 5 · 16,8 + 6,5 = 90,5 (т).
ОТВЕТ: вагон весит 16,8 т, электровоз - 90,5 т.