: Разложите выражения на множители 2) b-b^1/2 3) 3+3^1/3 4) (5x)^1/2+(3x)^1/2

👇

Ответ:

marinamarina24

20.07.2021

Объяснение:

x2 - 12х + 20. ... (7х + 1)(х – 3) + 20(х - 1)(х + 1) = 3(3х – 2)2 + 13. ... ( 2x – 7)(х + 1) + 3(4x — 1)(4х + 1) = 2(5х – 2)? - 53. ... 5x - 2y = 11;.

x = 11

4,7(86 оценок)

Открыть все ответы

Ответ:

ксюша1704

20.07.2021

1) Используя формулу n-го члена арифметической прогрессии 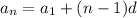a_n=a_1+(n-1)d , вычислим двадцатый член этой прогрессии:

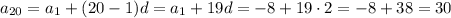
$a_{20}=a_1+(20-1)d=a_1+19d=-8+19\cdot2=-8+38=30$

ответ: 30.

2) Формула суммы первых n членов арифметической прогрессии следующая: 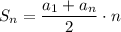$S_n=\dfrac{a_1+a_n}{2}\cdot n$

a_1=7;~~ d=a_2-a_1=11-7=4

Найдем же сначала восемнадцатый член арифметической прогрессии

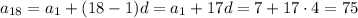
$a_{18}=a_1+(18-1)d=a_1+17d=7+17\cdot4=75$

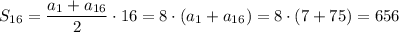
$S_{16}=\dfrac{a_1+a_{16}}{2}\cdot 16=8\cdot(a_1+a_{16})=8\cdot(7+75)=656$

ответ: 656.

3) Первый член: 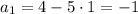$a_1=4-5\cdot1=-1$

Второй член: 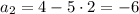$a_2=4-5\cdot2=-6$

Третий член: 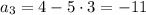$a_3=4-5\cdot3=-11$

Как видно, каждый последующий член уменьшается на (-5),т.е. это разность d = -5, следовательно, последовательность является арифметической прогрессией.

4) Используя n-ый член арифметической прогрессии, найдем ее разность

$a_{10}=a_1+(10-1)d=a_1+9d\\ d=\dfrac{a_{10}-a_1}{9}=\dfrac{-46+1}{9}=-5$

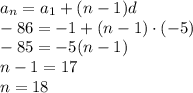
$a_n=a_1+(n-1)d\\ -86=-1+(n-1)\cdot(-5)\\ -85=-5(n-1)\\ n-1=17\\ n=18$

Да, является арифметической прогрессией.

5) Данная последовательность является арифметической прогрессии с первым членом a_1=2 и разностью прогрессии d=1

Всего таких членов не трудно посчитать по формуле n-го члена арифметической прогрессии:

$92=2+n-1\\ n=91$

То есть, нужно посчитать сумму первых 91 членов арифметической прогрессии

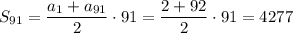
$S_{91}=\dfrac{a_1+a_{91}}{2}\cdot91=\dfrac{2+92}{2}\cdot91=4277$

ответ: 4277.

4,5(69 оценок)

Ответ:

SanzhikGanzhik

20.07.2021

1)
База индукции: 1

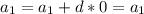a_1=a_1+d*0=a_1

проверено.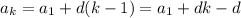

Предположим, что утверждение верно для n=k.
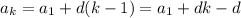$a_{k}=a_1+d(k-1)=a_1+dk-d$
Покажем, и докажем, что утверждение верно так же для n=k+1.
$a_{k+1}=a_1+d[(k+1)-1]=a_1+dk$
Так как , следуя предположению $a_{k}=a_1+d(k-1)=a_1+dk-d$ то прибавив к данному выражению d. Мы получим следующий член $a_{k+1}=a_1+d[(k+1)-1]=a_1+dk$ .
Т.е. предположение верно. Ч.Т.Д.

2)
$S_n= \frac{n[2a_1+d(n-1)]}{2}$
База : 1
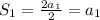Проверка: $S_1= \frac{2a_1}{2}=a_1$ .

Предположение: $n=k \Rightarrow S_k= \frac{k[2a_1+d(k-1)]}{2}= \frac{2a_1k+dk^2-dk}{2}$

Теперь покажем и докажем, что данное выражение верно и при n=k+1

:

Так как предыдущий член был равен k, то что бы узнать сумму первых k+1 членов, достаточно прибавить k+1 член (используя формулу которую мы доказали ранее):
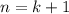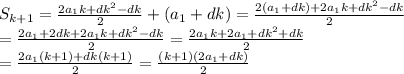
$S_{k+1}= \frac{2a_1k+dk^2-dk}{2}+(a_1+dk)= \frac{2(a_1+dk)+2a_1k+dk^2-dk}{2}\\= \frac{2a_1+2dk+2a_1k+dk^2-dk}{2}= \frac{2a_1k+2a_1+dk^2+dk}{2}\\
= \frac{2a_1(k+1)+dk(k+1)}{2}= \frac{(k+1)(2a_1+dk)}{2}$
т.е. мы пришли к изначальной формуле, если туда подставить k+1. Ч.Т.Д.

3)
Это не формула общего члена, это формула суммы.
При
q=1

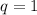получается деление на ноль, поэтому сразу пишем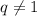 $q \neq 1$
База: 1
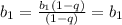
$b_1= \frac{b_1(1-q)}{(1-q)}=b_1$
Предположим, что формула верна для: n=k

Покажем и докажем что формула верна для n=k+1

:
Как и с суммой арифм.прогрессии. Мы добавим k+1 член к сумме.
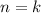
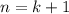$b_{k+1}= \frac{b_1(1-q^k)}{1-q}+b_1q^k= \frac{(1-q)b_1q^k+b_1(1-q^k)}{1-q}\\= \frac{b_1[(1-q)q^k+(1-q^k)]}{1-q}= \frac{b_1[q^k-q^{k+1}+1-q^k]}{1-q}= \frac{b_1(1-q^{k+1})}{1-q}$
Ч.Т.Д.

4,5(93 оценок)

Это интересно:

Хобби-и-рукоделие

05.06.2023

Изготовление сумки почтальона своими руками...

Кулинария-и-гостеприимство

03.12.2020

Кекс из простых ингредиентов: легко, быстро и вкусно!...

Здоровье

19.02.2020

Гель алоэ вера: эффективное средство от прыщей и других проблем кожи...

Компьютеры-и-электроника