У мальчика есть кубики трёх цветов. Он строит из этих кубиков башни, ставя каждый следующий кубик на предыдущий. Запрещено использовать более трёх кубиков каждого из цветов. Мальчик заканчивает стоить башню, как только в ней окажется по 3 кубика каких-то двух цветов. Сколько различных башен может построить мальчик?
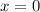– выколота.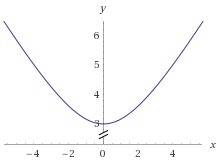
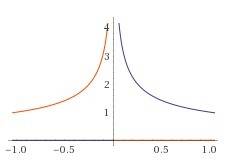
Наверняка существует и куда более простое и рациональное решение. Но я пока что нашёл такое. Для начала пусть есть 12 кубиков двух цветов - по 6 кубиков каждого цвета (для определённости пускай это будут 6 синих, и 6 красных), и пусть из них выстроена башня. Тогда для каждой такой башни наверх можно положить либо синий, либо красный кубик, и тогда построение башни тут же заканчивается: ведь по условию Коля заканчивает строить башню сразу же, как только в ней оказываются 7 кубиков одного цвета. Посчитаем, сколько таких башен существует. Если бы все кубики были разноцветными, то их было бы 12! Но в башне есть 6 синих кубиков и 6 красных кубиков, так что перестановка любой пары синих кубиков не даёт нам новую башню. 6 синих кубиков мы можем переставить и столько же для красных. Следовательно, общее число башен из 12 кубиков надо разделить ещё на 6!, а потом ещё раз на 6!. Получится 12! / (6! * 6!). И поверх каждой такой башни можно сверху положить либо синий, либо красный кубик - всего 2 комбинации, так что всего башен из 13 кубиков получается 2*12! / (6! * 6!) Теперь пусть есть башня из 6 синих кубиков и 5 красных кубиков. Если мы положим сверху синий кубик, то башня тут же заканчивается. Аналогично, когда есть башня из 5 синих кубиков и 6 красных, то она заканчивается, как только сверху оказывается ещё один красный кубик. Получается таким образом башня из 11 кубиков и ещё кубик сверху - и так 2 раза. Аналогично рассуждая, количество таких башен равно 11! / (6! * 5!), если синих кубиков 6, а красных 5 и столько же - наоборот. Всего: 2*11! / (6! * 5!) Далее, аналогично, для общего количества башен из 6 кубиков одного цвета и 4 кубиков другого всего есть вариантов 2*10! / (6! * 4!) (10! / (6! * 4!) для 6 кубиков синего цвета и 4 красного и столько же для случая наоборот). Для сочетания 6 - 3 (6 кубиков одного цвета и 3 другого) есть 2*9! / (6!*3!) вариантов. Для сочетания 6-2 есть 2*8! / (6! * 2!) вариантов Для сочетания 6-1 есть 2*7! / (6! * 1!) вариантов. И (формально продолжая закономерность), для сочетания 6-0 (все кубики одного цвета есть 2*6! / (6! * 0!) - всего 2 варианта (всего 7 кубиков, и все либо синие, либо красные). Остаётся только всё это сложить. Вынося общий множитель за скобку, получим: (2 / 6!) * (12! / 6! + 11! / 5! + 10! / 4! + 9! / 3! + 8! / 2! + 7! / 1! + 6! / 0!) - таково общее количество всевозможных башен, которые может построить Коля. Считаем: (2 / (1*2*3*4*5*6)) * (12*11*10*9*8*7 + 11*10*9*8*7*6 + 10*9*8*7*6*5 + 9*8*7*6*5*4 + 8*7*6*5*4*3 + 7*6*5*4*3*2 + 6*5*4*3*2*1) = (2 / (1*2*3*4*5*6)) * (7 * (12*11*10*9*8 + 11*10*9*8*6 + 10*9*8*6*5 + 9*8*6*5*4 + 8*6*5*4*3 + 6*5*4*3*2) + 1) Производим сокращения, не вычисляя эти произведения: 2 * (7 * (132 + 66 + 30 + 12 + 4 + 1) + 1) = 2 * (7 * 245 + 1) = 2 * (1715 + 1) = 2 * 1716 = 3432. Итого, 3432 различные башни.
Объяснение:ой:)