Определим общее число расстановок на пяти позициях 5 шариков:
Однако, среди этих расстановок есть недопустимые (то есть те, при которых между зеленым и желтым шариком располагаются два или более шарика). Найдем число недопустимых расстановок.
Найдем число недопустимых размещений зеленого и желтого шарика. Их можно просто перечислить:
1) зеленый на 1-ом месте, желтый на 4-ом месте
2) зеленый на 1-ом месте, желтый на 5-ом месте
3) зеленый на 2-ом месте, желтый на 5-ом месте
4) зеленый на 4-ом месте, желтый на 1-ом месте
5) зеленый на 5-ом месте, желтый на 1-ом месте
6) зеленый на 5-ом месте, желтый на 1-ом месте
В каждом из этих случаев оставшиеся три шарика могут размещаться на свободных местах
Таким образом, всего имеется недопустимых расстановок.
1) Область определения: x ∈ (-∞; ∞). 2) Четность-нечетность: Т.к. и , то функция является функцией общего вида. 3) Точки пересечения с Ox. Решим исходное уравнение при y = 0. (метод решения: Виета-Кардано) Получим один корень: x = 0.148 - абсцисса точки пересечения графка с осью Ox. Координаты точки: (0.148; 0)
Точка пересечения с Oy. Найдем y, подставив в уравнение x = 0. Получим: y = -5. Координаты точки: (0, -5).
4) Так как функция кубическая, то точек экстремума не имеет.
5) Первая производная.
2. Вторая производная. Находим корни уравнения. Для этого полученную функцию приравняем к нулю. Откуда точка перегиба: x = 5/3
и 
, то функция является функцией общего вида.
Определим общее число расстановок на пяти позициях 5 шариков:
Однако, среди этих расстановок есть недопустимые (то есть те, при которых между зеленым и желтым шариком располагаются два или более шарика). Найдем число недопустимых расстановок.
Найдем число недопустимых размещений зеленого и желтого шарика. Их можно просто перечислить:
1) зеленый на 1-ом месте, желтый на 4-ом месте
2) зеленый на 1-ом месте, желтый на 5-ом месте
3) зеленый на 2-ом месте, желтый на 5-ом месте
4) зеленый на 4-ом месте, желтый на 1-ом месте
5) зеленый на 5-ом месте, желтый на 1-ом месте
6) зеленый на 5-ом месте, желтый на 1-ом месте
В каждом из этих случаев оставшиеся три шарика могут размещаться на свободных местах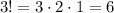
Таким образом, всего имеется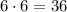
недопустимых расстановок.
Значит, допустимых расстановок имеется:
ответ: 84