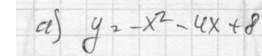
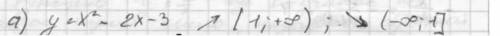

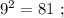 сумма количества цифр: 1 + 2 = 3 , количество цифр у квадрата числа вдвое больше количества цифр исходного числа.
сумма количества цифр: 1 + 2 = 3 , количество цифр у квадрата числа вдвое больше количества цифр исходного числа.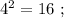 искомая сумма: 1 + 2 = 3 , количество цифр у квадрата числа всё так же вдвое больше количества цифр исходного.
искомая сумма: 1 + 2 = 3 , количество цифр у квадрата числа всё так же вдвое больше количества цифр исходного.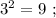 искомая сумма: 1 + 1 = 2 , количество цифр у квадрата равно количеству цифр исходного.
искомая сумма: 1 + 1 = 2 , количество цифр у квадрата равно количеству цифр исходного.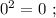 искомая сумма: 1 + 1 = 2 , количество у квадрата равно количеству цифр исходного.
искомая сумма: 1 + 1 = 2 , количество у квадрата равно количеству цифр исходного.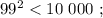 сумма: 2 + 4 = 6 , количество цифр у квадрата вдвое больше количества цифр исходного.
сумма: 2 + 4 = 6 , количество цифр у квадрата вдвое больше количества цифр исходного.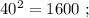 сумма: 2 + 4 = 6 , цифр у квадрата всё так же вдвое больше количества цифр исходного.
сумма: 2 + 4 = 6 , цифр у квадрата всё так же вдвое больше количества цифр исходного.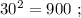 сумма: 2 + 3 = 5 , цифр у квадрата числа: 3 = 4–1 .
сумма: 2 + 3 = 5 , цифр у квадрата числа: 3 = 4–1 .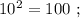 сумма: 2 + 3 = 5 , цифр у квадрата: 3 = 4–1 .
сумма: 2 + 3 = 5 , цифр у квадрата: 3 = 4–1 .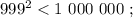 сумма: 3 + 6 = 9 , цифр у квадрата вдвое больше.
сумма: 3 + 6 = 9 , цифр у квадрата вдвое больше. сумма: 3 + 6 = 9 , цифр у квадрата вдвое больше.
сумма: 3 + 6 = 9 , цифр у квадрата вдвое больше.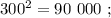 сумма: 3 + 5 = 8 , цифр у квадрата числа: 5 = 3*2–1 .
сумма: 3 + 5 = 8 , цифр у квадрата числа: 5 = 3*2–1 .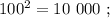 сумма: 3 + 5 = 8 , цифр у квадрата числа: 5 = 3*2–1 .
сумма: 3 + 5 = 8 , цифр у квадрата числа: 5 = 3*2–1 . сумма: 4 + 8 = 12 , у квадрата вдвое больше.
сумма: 4 + 8 = 12 , у квадрата вдвое больше.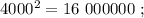 сумма: 4 + 8 = 12 , у квадрата вдвое больше.
сумма: 4 + 8 = 12 , у квадрата вдвое больше.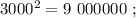 сумма: 4 + 7 = 11 , цифр у квадрата: 7 = 4*2–1 .
сумма: 4 + 7 = 11 , цифр у квадрата: 7 = 4*2–1 .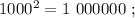 сумма: 4 + 7 = 11 , цифр у квадрата: 7 = 4*2–1 .
сумма: 4 + 7 = 11 , цифр у квадрата: 7 = 4*2–1 .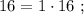
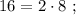
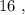 т.е.:
т.е.: 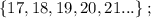
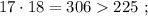
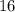 каждое – будет, очевидно, больше чем
каждое – будет, очевидно, больше чем 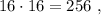 т.е. больше
т.е. больше 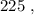 а значит, при выборе минимальных чисел в виде
а значит, при выборе минимальных чисел в виде  и
и 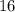 – подобрать остальные числа невозможно.
– подобрать остальные числа невозможно.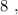 т.е.:
т.е.: 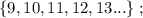
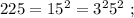
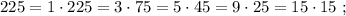
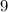 и
и 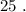
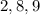 и
и 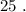
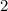 и
и 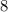 Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы 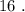
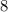 и
и 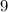 никаких натуральных чисел нет.
никаких натуральных чисел нет.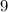 и
и 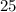 Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы 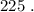
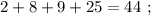
Я не. Н77еачагчешчк77е