Щоб знайти середню масу головки капусти навмання взяли 20 головок, маси яких виявилися:
2,8 кг; 2,8 кг; 2,9 кг; 3,1 кг; 3,2 кг; 3,1 кг; 3,3 кг; 3,2; 3,2 кг; 2,8 кг; 3,5 кг;
3,4 кг; 3,4 кг; 3,2 кг; 2,8 кг; 3,3 кг; 3,6 кг; 3,7 кг; 3,1 кг; 3,6 кг.
Знайти середню масу головки. Скласти статистичну таблицю.
Задача 2.
На заводі протягом семигодинного робочого дня робітник виготовляв
11, 9, 12, 13, 12, 10, 8 деталей. Записати впорядкований ряд. Знайти моду, медіану.
Задача 3.
За результатами тестування 48 студентів склали таблицю кількості допущених
помилок.
8 1 2 2 0 3 3 1 3 2 4 2
2 3 0 1 5 3 1 2 4 1 3 2
0 3 2 2 4 3 0 3 3 3 2 3
4 1 0 2 2 1 2 0 1 3 3 2
Скласти частотну таблицю і побудувати діаграму. Знайти центральні тенденції
вибірки.
Задача 4.
Результати вимірювання діаметра 200 деталей після шліфування занесено до
таблиці.
D, см 6,67-
6,69
6,69-
6,71
6,71-
6,73
6,73-
6,75
6,75-
6,77
6,77-
6,79
6,79-
6,81
6,81-
6.83
Кількість
деталей
5 17 24 54 52 23 18 7
Побудувати полігон частот, гістограму, визначити відносну частоту кожного
значення.
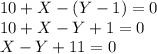
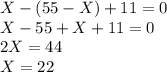
2X^2 - X * ( 2X - 2 ) = 6
2X^2 - 2X^2 + 2X = 6
2X = 6
X = 3
Y = 6 - 2 = 4
ОТВЕТ ( 3 ; 4 )
( X + 2 )*( Y + 1 ) = 12
X + 2Y = 6 ; X = 6 - 2Y
( 6 - 2Y + 2 )*( Y + 1 ) = 12
( 8 - 2Y )*( Y + 1 ) = 12
8Y + 8 - 2Y^2 - 2Y = 12
- 2Y^2 + 6Y - 4 = 0
- 2 * ( Y^2 - 3Y + 2 ) = 0
D = 9 - 8 = 1 ; √ D = 1
Y1 = ( 3 + 1 ) : 2 = 2
Y2 = ( 3 - 1 ) : 2 = 1
X1 = 6 - 4 = 2
X2 = 6 - 2 = 4
ОТВЕТ ( 2 ; 2 ) ; ( 4 ; 1 )
X^2 + Y^2 = 10
XY = - 3
X = ( - 3 / Y ) ; X^2 = 9 / Y^2
( 9 / Y^2 ) + Y^2 = 10
( 9 + Y^4 ) / Y^2 = 10 ( Y ≠ 0 )
9 + Y^4 = 10Y^2
Y^4 - 10Y^2 + 9 = 0
Y^2 = A ; A > 0
A^2 - 10A + 9 = 0
D = 100 - 36 = 64 ; √ D = 8
A1 = ( 10 + 8 ) : 2 = 9
A2 = ( 10 - 8 ) : 2 = 1
Y^2 = 9 ===> Y (1 /2 ) = ( + / - ) 3
Y^2 = 1 ===> Y ( 3/4 ) = ( +/ - ) 1
X^2 = 9 / Y^2
X^2 = 9 / 9 = 1 ===> X ( 1/2 ) = ( + / - ) 1
X^2 = 9 / 1 = 9 ===> X ( 3/4 ) = ( + / - ) 3
ОТВЕТ ( 1 ; 3 ); ( - 1 ; - 3 ); ( 3 ; 1 ) ; ( - 3 ; - 1 )