|x² - 16| + |x + 2| = 14 - x - x²
|(x - 4)(x + 4)| + |x + 2| = 14 - x - x²
x₁ = 4 ; x₂ = - 4 ; x₃ = - 2
1) x ∈ (- ∞ ; - 4)
x² - 16 -x - 2 = 14 - x - x²
2x² = 32
x² = 16
x₁ = - 4 - неуд
x₂ = 4 - неуд
2) x ∈ [ - 4 ; - 2)
- x² + 16 - x - 2 = 14 - x - x²
- x² - x - x + x² = 14 - 14
0 * x = 0
ответ : x ∈ [ - 4 ; - 2)
3) x ∈ [ - 2 ; 4)
- x² + 16 + x + 2 = 14 - x - x²
- x² + x + x + x² = 14 - 18
2x = - 4
x = - 2
4) x ∈ [4 ; + ∞)
x² - 16 + x + 2 = 14 - x - x²
x² + x + x + x² - 14 - 14 = 0
2x² + 2x - 28 = 0
x² + x - 14 = 0
D = 1² - 4 * (- 14) = 1 + 56 = 57
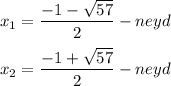
- 4 + (- 3) + (- 2) = - 9
ответ : - 9

Решение методом разложения:
Разложим числа на простые множители и подчеркнем общие множители чисел:
58110697294650 = 2 · 3 · 3 · 3 · 5 · 5 · 7 · 7 · 7 · 11 · 11 · 13 · 13 · 17 · 19 · 19
3191270940 = 2 · 2 · 3 · 3 · 3 · 5 · 11 · 11 · 13 · 13 · 17 · 17
Общие множители чисел: 2; 3; 3; 3; 5; 11; 11; 13; 13; 17
Чтобы найти НОД чисел, необходимо перемножить их общие множители:
НОД обоих чисел = 2 · 3 · 3 · 3 · 5 · 11 · 11 · 13 · 13 · 17 = 93860910
Решение методом Евклида:
1) 58110697294650 : 3191270940 = 18209 (ост. 844748190)
2) 3191270940 : 844748190 = 3 (ост. 657026370)
3) 844748190 : 657026370 = 1 (ост. 187721820)
4) 657026370 : 187721820 = 3 (ост. 93860910)
5) 187721820 : 93860910 = 2 без остатка.
Значит, 93860910 является НОД.
Примечание:
Проверку прикрепил фотографией.
ответ: НОД = 93860910.