
Для решения этой задачи используем формулы арифметической прогрессии.
а₁=5 [в первый день 5 капель]
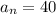 [день, в который нужно выпить 40 капель]
[день, в который нужно выпить 40 капель]
d=5 [разность арифметической прогрессии, т.к. каждый день дозировка увеличивается на одну и ту же величину - 5 капель]
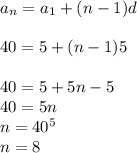
На восьмой день дозировка составит 40 капель.
По формуле суммы n первых членов арифметической прогрессии найдм сколько всего капель нужно выпить больному за 8 дней.
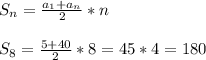
180 капель должен выпить больной за первые 8 дней лечения.
В последний период лечения больной должен уменьшать дозировку каждый день на 5 капель, и с дозировки в 40 капель дойти до 5 капель.
На это ему понадобиться 8 дней (также, как и в первый период лечения).
Суммарное количество капель, которые должен выпить больной за эти 8 дней, составит 180.
В середине лечения больной должен три дня подряд пить по 40 капель. Два раза по 40 капель мы уже учли. Поэтому к общей сумме добавим только 40.
180+180+40 = 400 (капель) - должен выпить больной за весь период лечения.
В одном пузырьке содержится 200 капель лекарства. Значит больному нужно купить 400:200 = 2 пузырька лекарства.
ответ: 2 пузырька.
Условие существования логарифма: 3x + 1 > 0 ⇒ x >
По свойству логарифма: logₐb - logₐc = logₐ
Т.к. логарифмическая функция каждое свое значение принимает единожды,
Мы уже ставили условие, что x - 1 > 0, тогда
3x + 1 = (x - 1)²
3x + 1 = x² - 2x + 1
x² - 5x = 0
x(x - 5) = 0
x = 0 или x = 5.
Вспоминаем, что x > 1, и получаем x = 5.
ответ: 5.
2) 25ˣ - 6 * 5ˣ = -5
Знаем, что 25 = 5², значит, уравнение принимает такой вид:
(5²)ˣ - 6 * 5ˣ = -5
По свойству дробей (5²)ˣ раскрывается, как 5²ˣ, и можем представить в виде (5ˣ)², значит,
(5ˣ)² - 6 * 5ˣ = -5
Пусть t = 5ˣ, тогда
t² - 6t + 5 = 0
t = 1 или t = 5.
Обратная замена:
5ˣ = 1 или 5ˣ = 5, т. е. x = 0 или x = 1.
ответ: 0; 1.