1) Не буду переписывать всю систему, начну с решения.
выразим через второе уравнение y:
y=2-5x
подставим y в первое уравнение:
2x-3(2-5x)=11
2x-6+15x=11
17x=17
x=1
Найдем y:
y=2-5*1=-3
ответ: (1;-3).
2) Решим первое неравенство:
1-6x<10
6x>-9
x>-9/6
x>-1,5 - это решение первого неравенства.
Решим второе неравенство:
5x-7<x-7
4x<0
x<0 - это решение втрого неравенства.
Общая часть интервалов (-1,5; +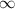
) и (-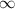;0) является промежуток (-1,5;0).
ответ: (-1,5;0).
Пусть x = r1, y = r2, x^1/2 + y^1/2 = r3 - заданные в условии рациональные числа.
Тогда
x - y = (x^1/2 - y^1/2)(x^1/2 + y^1/2) - по формуле разложения для разности квадратов. Поскольку x - y = r1 - r2 = r4 - разность двух рациональных чисел есть число рациональное, и x^1/2 + y^1/2 = r3 - рациональное число (по условию), то x^1/2 - y^1/2 = r4/r3 = r5 - частное двух рациональных чисел есть также число рациональное.
Итак,
x^1/2 - y^1/2 = r5 - рациональное число (1)
x^1/2 + y^1/2 = r3 - рациональное число (по условию) (2)
Слкладывая обе части уравнений (1) и (2) получим, что х^1/2 = (r3 + r5)/2 - рациональное число (как сумма и частное рациональных чисел).
Аналогично, вычтя обе части уравнения (2) из обеих частей уравнения (1) получим, что y^1/2 = (r3 - r5)/2 - рациональное число (как разность и частное рациональных чисел).
Таким образом мы доказали, что числа х^1/2 и y^1/2 являются рациональными.
Будет -2401 или 2401
Объяснение:
чтобы возвести степень в степень основание переписываем, а показатели перемножаем. Получает 7 в минус 6 степени- в числителе и 7 в минус 10 - в знаменателе. 7 в минус 10 это 7 в минус 6 на 7 в минус 4(раскладываем). Потом у нас сокращается 7 в минус 6 и остается 7 в минус 4, а это -2401