Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам. Следовательно, если их провести, то получим 4 равных прямоугольных треугольника с катетами 3 см и 4 см (6 см : 2 = 3 см и 8 см : 2 = 4 см).
По теореме Пифагора найдем сторону ромба из одного из получившихся прямоугольных треугольников (обозначим ее а): а² = 3² + 4² = 9 + 16 = 25 = 5², значит, сторона ромба 5 см.
Можно и по-другому. Прямоугольный треугольник со сторонами 3, 4 и 5 - египетский (известен еще древним египтянам). Т.к. у нас есть прямоугольный треугольник с катетами 3 см и 4 см, то гипотенуза равна 5 см.
1) -3
6) -2
Объяснение:
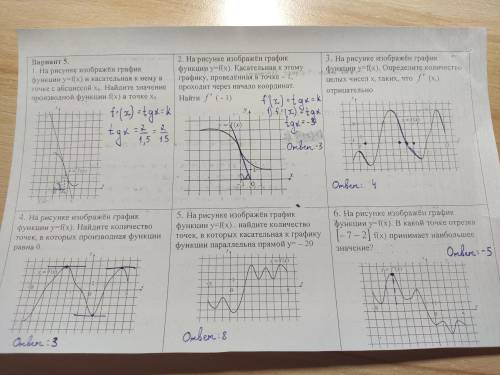
В первом задании (рис.1) нужно взять любые 2 точки на касательной и достроить до прямоугольного треугольника. Получается tgβ=3/1=3.
Но касательная убывает (образует тупой угол с осью Ох), значит производная в данной точке отрицательна! Значит нужный нам угол - это α
tgα=-tgβ=-3
№6 (рис.2)
в задании опечатка, так как на рисунке дан график ПРОИЗВОДНОЙ ( y=f'(x) )
Если производная лежит выше оси Ох, то она положительна.
Если производная положительна, то сама функция возрастает!
А если функция возрастает на отрезке [-7; -2], то ее наибольшее значение в крайней правой точке.