ОДЗ: x>0; y>0; y≠1; y>2x.
Преобразуем второе уравнение:
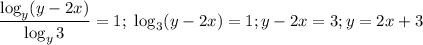
(мы дважды воспользовались формулой перехода к другому основанию). Прологарифмируем первое уравнение по основанию y:
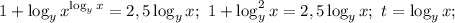
Можно было бы спокойно решить это квадратное уравнение с дискриминанта, но это скучно. Поступлю не самым простым образом. Очевидно. что t≠0. Делим уравнение на t и записываем его в виде
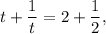что сразу подсказывает решения t=2 и 
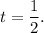Других решений быть не может - все-таки у нас квадратное уравнение!
1) t=2;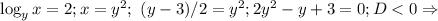 
решений нет.
2) 
(отрицательный корень отбрасываем по ОДЗ); y=9. На всякий случай делаем проверку подстановкой в уравнение и выписываем ответ.
ответ: (3;9)
Sin(x - 2) = sin x - sin 2 sin x*cos 2 - cos x*sin 2 = sin x - sin 2 0 = sin x*(1 - cos 2) + cos x*sin 2 - sin 2 Переходим к половинным аргументам 2sin(x/2)*cos(x/2)*(1 - cos 2) + sin 2*(cos^2(x/2) - sin^2(x/2)) - - sin 2*(cos^2(x/2) + sin^2(x/2)) = 0 -sin^2(x/2)*(sin 2 + sin 2) + 2sin(x/2)*cos(x/2)*(1 - cos 2) + + cos^2(x/2)*(sin 2 - sin 2) = 0 -2sin 2*sin^2(x/2) + 2sin(x/2)*cos(x/2)*(1 - cos 2) = 0 2sin(x/2)*(cos(x/2)*(1 - cos 2) - sin(x/2)*sin 2) = 0 1) sin(x/2) = 0; x/2 = pi*k; x = 2pi*k 2) cos(x/2)*(1 - cos 2) - sin(x/2)*sin 2 = 0 cos(x/2)*(1 - cos 2) = sin(x/2)*sin 2 tg(x/2) = (1 - cos 2)/sin 2 x/2 = arctg((1 - cos 2)/sin 2) + pi*n x = 2arctg((1 - cos 2)/sin 2) + 2pi*n Еще подходит x = 2 sin (2 - 2) = sin 2 - sin 2 sin 0 = 0