Согласно теореме Виета, сумма корней квадратного уравнения равна отрицательному коэффициенту b:
x1 + x2 = -b
Произведение корней квадратного уравнения в этой же теореме равно свободному коэффициенту с:
х1 × х2 = с
Доказательство:
Возьмём следующее уравнение:
х² + 6х - 7 = 0
Сначала решим его через дискриминант:
D = b² - 4ac = 36-4×(-7) = 36+28 = 64
x1,2 = (-b±√D)÷2a = (-6±8)÷2
x1 = (-6+8)÷2 = 1
x2 = (-6-8)÷2 = -7
Теперь решим это же уравнение через теорему Виета:
Мы знаем, что:
х1 + х2 = -b
x1 × x2 = c
Осталось лишь подобрать такие корни уравнения, которые бы подходили под эти два равенства. Путём нехитрых вычислений, находим, что этими корнями являются числа -7 и 1:
-7 + 1 = -6 = -b
-7×1 = -7 = c
ответы сходятся, значит наши рассуждения верны.
Это работает со всеми квадратными уравнениями, в которых коэффициент а = 1.
Теорема доказана.
ответ: 1) 9/28; 2) 5/14.
Пошаговое объяснение:
1) А — сумма цифр на кости домино менее 4;
Общее число возможных исходов элементарных исходов равно числу которыми можно взять одну кость домино из 28
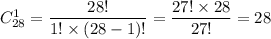
Число исходов, благоприятствующих событию А: нужно найти количество всех костей домино, в которой сумма цифр взятой кости домино менее 4.
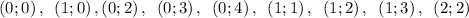
Т.е. число исходов, благоприятствующих событию А, равно 9.
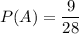— вероятность того, что сумма цифр на ней менее 4.
2) Общее число возможных исходов элементарных исходов равно 28(с пункта 1).
B — обе цифры на ней четные.
Число исходов, благоприятствующих событию В равно числу достать одну кость домино с четными цифрами.
Всего таких костей домино: 10 (из перечень костей домино на картинке легко увидеть)
Вероятность события В: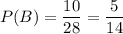 
30
Объяснение:
Из второго уравнения
b=a
Поставляем в первое уравнение
5a+a=180
6a=180
a=30
Отсюда
b=30