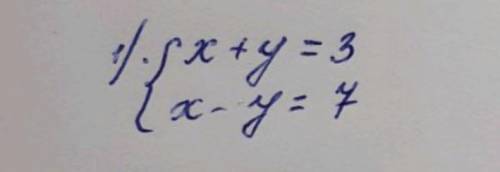
В текстовых задачках нужно вводить переменную X, то что вопрос спрашивается
Узнаем какую скорость хотел изначально(планировал)
T*V=S
80/x - время за которое он планировал
80/10+x - время за которое он в итоге
>>>Он был остановлен у сфетафора на 16 мин(по условию задачи)
>>>16 минут переводим в часы, по скольку скорость в часах т.е делим на 60
16/60 сокращаем на 4
4/15
>>>составляем уровнение, чтобы найти скорость по графику
80/x - 80/x+10=4/15
80(10+x) - 80x / x(10+x)= 4/15
800+80x-80x / 10x + x^2 = 4/15
>>> 80x сокращается
800 / 10x+x^2 = 4/15
>>> переуножаем дробь крест на крест.
800*15=40x + 4x^2
4x^2 + 40x - 12000=0
>>> делим обе части на 4
x^2 +10x - 3000=0
>>> Находим через дискриминант x
D=b^2-4ac=100-4=12100
x1; x2 = -b ± Корень из дискриминанта / 2a
x1 = -10-110/2= -60
(по скольку это скорость оно минусом не может ровняться)
x2 = -10+110/2 = 50
ответ: 50км/x
log_2(x^2+4x+3)=3 ОДЗ: x^2+4x+3>0
x^2+4x+3=2³ x^2+4x+3=0
x^2+4x+3=8 x₁+x₂=-4
x^2+4x-5=0 x₁*x₂=3
x₁+x₂=-4 x₁=-1; x₂=-3
x₁*x₂=-5 x∈(-∞;-3)∪(-1;+∞)
x₁=1
x₂=-5
2)
log_2(x^2-4x+2)=1 ОДЗ: x^2-4x+2>0
x^2-4x+2=2¹ x^2-4x+2=0
x^2-4x+2=2 D=-4²-4*1*2=8
x^2-4x=0 x₁=2+√2
x(x-4)=0 x₂=2-√2
x=0 или x∈(-∞;(2-√2))∪((2+√2;+∞)
x-4=0 => x=4
x₁=0
x₂=4
3)
log_18(x)=log_18(4)-9log_18(1) ОДЗ: x>0
log_18(x)=log_18(4/1⁹)
log_18(x)=log_18(4)
x=4
4)
log_27(x)=1/3 ОДЗ: x>0
x=27^1/3
x=∛(27)
x=3