8
Объяснение:
Сложим два равенства, получим уравнение:
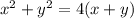
Раскроем скобки справа, перенесем влево и дополним до полных квадратов относительно х и у:
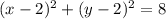
Выражаем x через y:
(вообще, правильнее было бы рассмотреть два случая: когда перед корнем стоит знак плюс, что мы и делаем, и когда перед ним стоит знак минус, но нас интересует максимальное значение, логичнее было бы рассмотреть только положительное значение)
Наша целевая функция, в которой будем находить максимум, имеет вид:
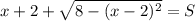, где S - сумма решений системы уравнений.
Найдем производную по х, приравняем к нулю эту функцию
Получим
Таким образом, мы сможем найти y: y₁ = 4; y₂ = 4
Стало быть, только в точке (4;4) достигается этот максимум суммы, которая равна 4+4 = 8
В обоих случаях рассматриваем прямоугольный треугольник с одним из углов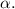 
В первом случае примем прилежащий к углу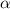 
катет за 3, а гипотенузу - за 5. Тогда неизвестный катет вычислим по т. Пифагора как 
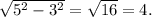Синус угла 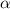есть отношение противолежащего катета к гипотенузе, т.е. 4/5. Тангенсом - отношение противолежащего катета к прилежащему, т.е. 4/3. Котангенсом - отношение прилежащего катета к противолежащему, т.е. 3/4.
Во втором случае примем катет, лежащий против 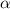за 4, а гипотенузу - за 5. Неизвестный катет, по теореме Пифагора, будет равен 3. Косинусом 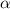есть отношение прилежащего катета к гипотенузе, т.е. 3/5. Тангенсом - отношение противолежащего катета к прилежащему, т.е. 4/3. Котангенсом - отношение прилежащего катета к противолежащему, т.е. 3/4.
1. Область определения: D(y)= X≠ 3 , X∈(-∞;3)∪(3;+∞). Не допускаем деления на 0 в знаменателе.
2.Поведение на бесконечности. Y(-∞)= -∞, Y(+∞)= -∞ - горизонтальная асимптота - y = 0.
3. Разрыв II-го рода при Х = 3.
Вертикальных асимптота - Х = 3.
4. Нули функции, пересечение с осью ОХ.
x-3 = 2. x = -2/3 .
5. Интервалы знакопостоянства.
Отрицательна: Y(x)<0 - X∈(-∞;3). Положительна: Y>0 - X∈(3;+∞;)
6. Проверка на чётность. Есть сдвиг по оси ОХ - нет симметрии ни осевой ни центральной.
Функция ни чётная, ни нечётная: Y(-x) ≠ -Y(x) , Y(-x)≠ Y(x).
7. Поиск экстремумов по первой производной.
y'(x) = - 2/(x-3)² = 0. Корней - нет
8. Локальный максимум - нет.
9. Интервалы монотонности.
Убывает: X∈(-∞;3)∪(3;+∞) - везде, где существует.
10. Поиск перегибов по второй производной.
y"(x) = 4/(x-3)³ = 0
Точки перегиба нет, кроме разрыва при Х = 0.
11. Вогнутая - "ложка"- X∈(3;+∞;), выпуклая - "горка" - X∈(-∞;3); 12. Наклонная асимптота.
k = lim(+∞) Y(х)/x = 2/(x²-3*х) = 0 - наклон. y = 0 - горизонтальная асимптота.
13. Область значений. E(y) - y∈(-∞;+∞).
14. График функции на рисунке в приложении.