Два рабочих могут выполнить заказ за 12 дней.Если половину работы выполнит первый рабочий,а затем его сменит второй рабочий,то весь заказ будет выполнен за 25 дней.За сколько дней каждый рабочий в отдельности выполнит данный заказ!
Решение
За х дней первый рабочий в отдельности выполнит данный заказ
за у дней второй рабочий в отдельности выполнит данный заказ
Пусть 1 - объём всего заказа (т.е. вся работа), тогда
1/х - часть работы, которую выполняет первый рабочий за 1 день (т.е. производительность первого)
1/у - производительность второго рабочего за 1 день
Первое уравнение получаем через общую производительность:
1/х + 1/у = 1/12
Упростив, получим:
12(х+у) = ху
Для второго уравнения найдем время, за которое выполнит половину всего заказа 1/2 каждый рабочий, работая в отдельности:
1/2 : 1/х = х/2 дней - это время за которое половину работы выполнит первый рабочий
1/2 : 1/у = у/2 дней - это время за которое половину работы выполнит второй рабочий
Получаем второе уравнение:
х/2 + у/2 = 25
Упростив, получим:
х + у = 50
Решаем систему:
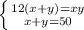
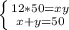
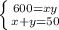
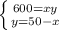
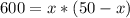
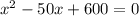
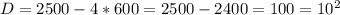
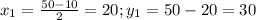
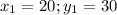
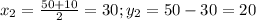
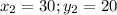
ответ: 20; 30
Найдём несколько следующих чисел данной последовательности, чтобы найти закономерность.
2) 7²=49; 4+9=13; 13+1=14
На втором месте стоит число 14
3) 14²=196; 1+9+6=16; 16+1=17
На третьем месте стоит число 17
4) 17²=289; 2+8+9=19; 19+1=20
На четвёртом месте стоит число 20
5) 20²=400; 4+0+0=4; 4+1=5
На пятом месте стоит число 5
6) 5²=25; 2+5=7; 7+1=8
На шестом месте стоит число 8
7) 8²=64; 6+4=10; 10+1=11
На седьмом месте стоит число 11
8) 11²=121; 1+2+1=4; 4+1=5
На восьмом месте стоит число 5
Получается, что теперь члены последовательности будут повторяться:
5; 8; 11; 5; 8; 11...
Получается последовательность:
7; 14; 17; 20; 5; 8; 11; 5; 8; 11...
Подсчитаем, какое число будет стоять на 2017 месте.
Вычтем 4 первых члена, которые не повторяются:
2017 - 4 = 2013
Число 2013 делится без остатка на 3
2013 : 3 = 671
Следовательно, после четырёх первых членов 7; 14; 17; 20 будет 671 раз повторяться тройка чисел 5; 8; 11. Значит, последним будет число 11.