Объяснение:
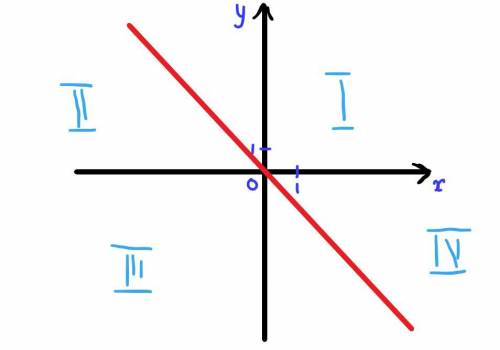
y = -x
1) Функция имеет единственный ноль к точке (0, 0)
2) Область определения функции ( -∞ ; +∞)
3) Область значений такая же, т.е. ( -∞ ; +∞)
4) Область определения совпадает с областью значений
5) Функция располагается в 2 и 4 четвертях
6) Функция положительна ТОГДА И ТОЛЬКО ТОГДА, когда её аргумент отрицателен
7) Функция отрицательна ТОГДА И ТОЛЬКО ТОГДА, когда её аргумент положителен
8) Это монотонно убывающая функция
9) Функция убывает на всей своей области определения
10) Функция не имеет периода
11) График этой функции - прямая, проходящая через центр координат
12) Это нечётная функция
13) Тангенс угла наклона касательной к точке графика постоянен и равен -1 для всех х
14) Площадь под графиком от 0 до х равна 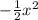
Здесь все свойства функции, выбирайте нужные.
На графике красным - сам график
Голубым подписаны четверти, их подписывать не обязательно.
64 (км/час) - собственная скорость лодки
4 (км/час) - скорость течения реки
Объяснение:
Задача:за 5 часов по течению и 1 час 30 мин против течения моторная лодка проплывает 430 км. За 1 час 30 мин против течения моторная лодка проплывает 90 км. Найдите собственную скорость лодки и скорость течения реки .
х - собственная скорость лодки
у - скорость течения реки
(х+у) - скорость лодки по течению
(х-у) - скорость лодки против течения
Составляем систему уравнений согласно условию задачи:
Формула движения: S=v*t
S - расстояние v - скорость t - время
(х+у)*5+(х-у)*1,5=430
(х-у)*1,5=90
Раскроем скобки:
5х+5у+1,5х-1,5у=430
1,5х-1,5у=90
Приведём подобные члены:
6,5х+3,5у=430
1,5х-1,5у=90
Выразим х через у во втором уравнении, подставим выражение в первое уравнение и вычислим у:
1,5х=90+1,5у/1,5 разделим уравнение на 1,5 для удобства вычислений:
х=60+у
6,5(60+у)+3,5у=430
390+6,5у+3,5у=430
10у=430-390
10у=40
у=4 (км/час) - скорость течения реки
х=60+у
х=60+4
х=64 (км/час) - собственная скорость лодки
Проверка:
68*5+60*1,5=430
60*1,5=90, верно.
5а
Объяснение:
Из первого уравнения
x/y=a x=a*y
Из второго уравнения
Y/z=5 z=y/5
Тогда
X/z=a*y/(y/5) при сокращении получаем 5а