Объяснение:
Чтобы узнать какой цифрой оканчивается число:
Делим показатель степени на число вариантов, тоесть на количество цифр, которыми может оканчиваться число в разных целых положительных степенях, далее смотрим по остатку, который останется (или не останется. если нацело) при делении.
Рассмотрим отдельно каждое слагаемое данной суммы.
54¹=54, оканчивается на 4 (первый вариант, если при делении, указанном выше, остаток получится 1)
54²= 2916, оканчивается на 6 (второй вариант, если при делении остаток получится 2 (нацело))
Вариантов 2.
35÷2= 17 (остаток 1), тогда нам подходит первый вариант, тоесть 54³⁵ будет оканчиваться на 4.
Рассмотрим 28²¹
28¹=28, оканчивается на 8 (первый вариант, если получится остаток 1)
28²=784, оканчивается на 4 (второй вариант, если выйдет остаток 2)
28³=21952, оканчивается на 2 (третий вариант, если получится остаток 3)
28⁴=614656, оканчивается на 6 (четвертый вариант, если получится остаток 4 (нацело))
Вариантов 4.
21÷4=5 (остаток 1), значит первый вариант, тоесть 28²¹ будет оканчиваться на 8.
Сложим последние цифры чисел в степенях.
4+8=12, оканчивается на 2.
Значит 54³⁵ + 28²¹ оканчивается на 2
ответ: 2
а) sin x - 0,5 = 0
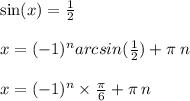
*где n - целое число
Рассмотрим варианты:
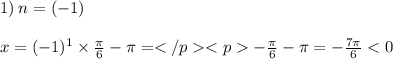
При n=(-1) - х<0 и не принадлежит отрезку [0;2π].
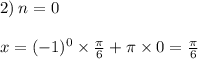
При n=0 - x = π/6 - принадлежит отрезку [0;2π].
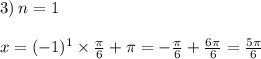
При n=1 - x = (5π/6) - принадлежит отрезку [0;2π].
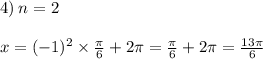
При n=2 - x = (13π/6) - не принадлежит отрезку [0;2π].
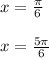
б) tg x - 1 = 0
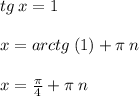
*где n - целое число
Рассмотрим варианты:
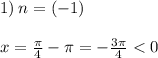
При n=(-1) - х<0 и не принадлежит отрезку [0;2π].
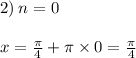
При n=0 - x = π/4 - принадлежит отрезку [0;2π].
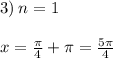
При n=1 - x = (5π/4) - принадлежит отрезку [0;2π].
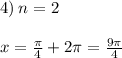
При n=2 - x = (9π/4) - не принадлежит отрезку [0;2π].
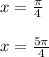
![Найдите корни уравнения, принадлежащие отрезку [0;2пи]: а) sin x - 0,5 = 0; б) tg x - 1 = 0.](/tpl/images/4836/4198/1fe1b.jpg)