Уравнение прямой, проходящей через точки ( -5,-2) и (-2,0) имеет вид y=kx+b:
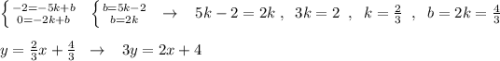
Уравнение окружности с центром в точке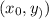 
и радиусом, равным R, имеет вид: 
.
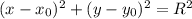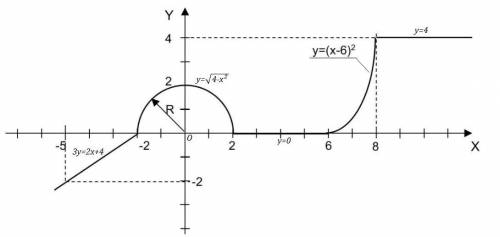
Тогда окружность на рисунке имеет вид:
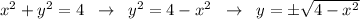
Если перед корнем берём знак (+), то получаем уравнение верхней полуокружности (y≥0) , а если берём знак (-), то получаем уравнение нижней полуокружности (у≤0) .
Уравнение прямых, проходящих параллельно оси ОХ через точку с координатами (a,b) , имеет вид: у=b .
Аналитически заданная на графике функция имеет вид:
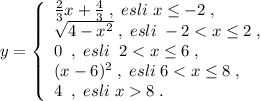
чтобы исследовать функцию на экстремум, надо найти ее производную
у=(х-1)²/х²
это дробь, а производная дроби равна разности произведения производной числителя на знаменатель и произведения числителя на производную знаменателя, деленной на квадрат знаменателя.
у¹ = ((х-1)¹*х² - (х-1)²*(х²)¹)/х⁴= (2х²-2х)/х⁴
у¹=0 - условие экстремума функции
(2х²-2х)/х⁴=0
х≠0 - на ноль делить нельзя
2х²-2х=0
х=0 и х=1 -ноль не подходит, берем 1
Чтобы функция имела в точке экстремум надо, чтобы при переходе через точку она меняла знак
вычислим
у(1/2) = 1 > 0
у(2) = 1/4 > 0
знак не поменялся, значит экстремума в этой точке нет.
в точке х=0, в которой функция не определена тоже нет перемены знака
у(-1) = 4 > 0 и у (1/2) = 1 > 0
ответ: функция экстремумов не имеет.
x=0.8, y= - 1.4
Объяснение:
3x+2x+y-y=4
5x=4
x=0.8
y= 2*0.8-3=1.4