Запишем эту сумму для произвольного числа слагаемых:
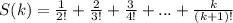
Вычислим значения S(k) для нескольких значений k:
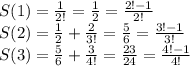
Тогда можно предположить, что
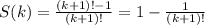
Но это ещё надо доказать. Используем индукцию. Выше было показано, что равенство верно для первых 3 натуральных k. Докажем, что из справедливости равенства для k=n следует справедливость равенства для k=n+1, тогда равенство можно будет считать справедливым для всех натуральных k.
Итак, предположим, что справедливо равенство
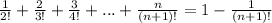
Проверим, верно ли, что
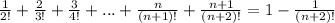
Подставляем сюда предыдущее выражение:
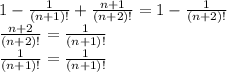
Получили верное равенство. Теперь можно вычислить значение нашей суммы:
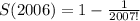
У нас могут быть такие знаменатели.
1 только числа. разные, тогда наименьшим общим знаменателем будет НОК этих чисел.
2. Только буквы, различные, или их сумма, что касаемо букв, то мы берем общую букву с НАИБОЛЬШИМ показателем, потому что Вам потом придется ее делить на остальные знаменатели.
3. У вас есть в знаменателях произведение букв и чисел. Как в этом случае найти общий знаменатель? Если среди букв нет общих, их надо просто все перемножить. Если есть общие, как я писал раньше, надо брать общую букву с наибольшим показателем. А из чисел всегда ищем НОК - наименьшее общее кратное.
Нашли общий знаменатель. Что дальше? Дальше делите на все знаменатели этот общий получаете дополнительные множители, и цепляете дополнительные множители к каждой дроби. Умножаете эти доп. множители на числители, знаменатели уже общие есть.
Складываете числители. Или вычитаете числители. смотрите, если получились сократимые дроби, сокращаете.
Это курс молодого бойца Вам на память. Удачи.