Заданные в условии числа - это угловые меры в радианах.
360° = 2π ≈ 6,28 радиан полный оборот.
180° = π ≈ 3,14 радиан - развёрнутый угол.
90° = π/2 ≈ 1,57 радиан - прямой угол.
На числовой окружности отсчёт углов начинается от положительного направления оси ОХ : положительные угловые меры против часовой стрелки, отрицательные - по часовой стрелке. Чтобы построить точку на окружности, можно перевести радианы в градусы и воспользоваться транспортиром.
Линейное уравнение [приведенное к типу ах=b, где a,b - некоторые числа] имеет бесконечное множество корней когда a=0; b=0 в нашем случае а значит такой случай бесконечного множества корней для данного уравнения с параметром не возможен
------ иначе пусть А+8=0, т..е. A=-8 , тогда уравнение имеет вид 0х=-15 - а значит не имеет корней (так как 0х=0, а 0 не равно -15)
если же то тогда уравнение имеет один единственный корень
рассмотрены все возможные случае, а значит случай бесконечного множества корней для данного уравнения с параметром не возможен
Заданные в условии числа - это угловые меры в радианах.
360° = 2π ≈ 6,28 радиан полный оборот.
180° = π ≈ 3,14 радиан - развёрнутый угол.
90° = π/2 ≈ 1,57 радиан - прямой угол.
На числовой окружности отсчёт углов начинается от положительного направления оси ОХ : положительные угловые меры против часовой стрелки, отрицательные - по часовой стрелке. Чтобы построить точку на окружности, можно перевести радианы в градусы и воспользоваться транспортиром.
а)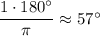
0° < 57° < 90° ⇒ 1 в первой четверти
б)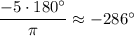 ; -286° + 360° = 74°
; -286° + 360° = 74°
0° < 74° < 90° ⇒ (-5) в первой четверти
в)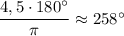
180° < 258° < 270° ⇒ 4,5 в третьей четверти
г)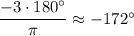
-180° < -172° < -90° ⇒ (-3) в третьей четверти