Дана функция 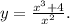
Производная её равна: y' = (3x^2*x^2 - 2x*(x^3 + 4))/x^4 = (x^3 - 8)/x^3.
Приравняем её нулю ( при х не равном 0 можно только числитель).
x^3 - 8 = 0.
x^3 = 8, х = ∛8 = 2. Это критическая точка.
С учётом разрыва функции при х = 0 имеем 3 промежутка монотонности функции: (-∞; 0), (0; 2) и (2; +∞).
На промежутках находим знаки производной.
Находится производная, приравнивается к 0, найденные точки выставляются на числовой прямой; к ним добавляются те точки, в которых производная не определена.
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = -1 0 1 2 3
y' = 9 - -7 0 0,7037.
• Минимум функции в точке: х = 2, у = 3.
• Максимума функции нет.
• Возрастает на промежутках: (-∞; 0) U (2; ∞).
• Убывает на промежутке: (0; 2).
Дана функция 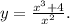
Производная её равна: y' = (3x^2*x^2 - 2x*(x^3 + 4))/x^4 = (x^3 - 8)/x^3.
Приравняем её нулю ( при х не равном 0 можно только числитель).
x^3 - 8 = 0.
x^3 = 8, х = ∛8 = 2. Это критическая точка.
С учётом разрыва функции при х = 0 имеем 3 промежутка монотонности функции: (-∞; 0), (0; 2) и (2; +∞).
На промежутках находим знаки производной.
Находится производная, приравнивается к 0, найденные точки выставляются на числовой прямой; к ним добавляются те точки, в которых производная не определена.
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = -1 0 1 2 3
y' = 9 - -7 0 0,7037.
• Минимум функции в точке: х = 2, у = 3.
• Максимума функции нет.
• Возрастает на промежутках: (-∞; 0) U (2; ∞).
• Убывает на промежутке: (0; 2).
n1 = int(input("вывод простых чисел от числа "))
n2 = int(input("до числа "))
a = [0] * n2 # создание массива с n2 количеством элементов
for i in range(n2): # заполнение массива ...
a[i] = i # значениями от 0 до n-1
# вторым элементом является единица, которую не считают простым числом
a[1] = 0
m = 2 # замена на 0 начинается с 3-го элемента (первые два уже нули)
while m < n2: # перебор всех элементов до заданного числа
if a[m] != 0: # если он не равен нулю, то
j = m * 2 # увеличить в два раза (текущий элемент простое число)
if a[m]>n1:
print (a[m])
while j < n2:
a[j] = 0 # заменить на 0
j = j + m # перейти в позицию на m больше
m += 1
Объяснение:
Вводим с клавиатуры, начиная с которого числа нам нужно будет выводить простые числа. В нашем случае - 40
Вводим до которого значения следует искать простые числа, в нашем случае - до 60.
На печати получим 5 простых чисел в заданном диапазоне.
Это не самое изящное решение. К тому же я не понял, что значит "введите их в произвольном порядке" - куда ввести?
Программа ищет простые числа с "решета Эратосфена" и выводит их на печать.