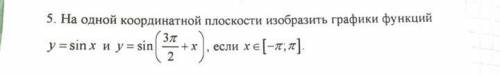
1) 15y²+6y =5y+2
15y²-5y+6у-2=0
5у(3у-1)+2(3у-1)=0
(3у-1)(5у+2)=0
3у-1=0 5у+2=0
3у=1 5у=-2
у=1/3 у=-2/5
ответ: -2/5; 1/3.
2) y³-2y²+у-2=0
y²(у-2)+(у-2)=0
(у-2)(y²+1)=0
у-2=0 y²+1=0
у=2 y²=-1 нет корней, так как квадрат всегда неотрицательное число
ответ: 2.
3) y³+6y²-y-6=0
y²(у+6)-(у+6)=0
(у+6)(y²-1)=0
у+6=0 y²-1=0
у=-6 y²=1
у=1 и у=-1
ответ: -1; 1; 2.
4) y³-12=3y²-4y
y³-3y²+4у-12=0
y²(у-3)+4(у-3)=0
(у-3)(y²+4)=0
у-3=0 y²+4=0
у=3 y²=-4 нет корней, так как квадрат всегда неотрицательное число
ответ: 3.
Координаты точки пересечения графиков данных функций (1; 1)
Решение системы уравнений х=1
у=1
Объяснение:
3х+y=4
7х—2у=5 решить графически систему уравнений.
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Прежде преобразуем уравнения в более удобный для вычислений вид:
3х+y=4 7х—2у=5
у=4-3х -2у=5-7х
2у=7х-5
у=(7х-5)/2
Таблицы:
х -1 0 1 х -1 0 1
у 7 4 1 у -6 -2,5 1
Согласно графика, координаты точки пересечения графиков данных функций (1; 1)
Значения таблиц это подтверждают.
Решение системы уравнений х=1
у=1
На картинке.
Объяснение: