1)Определение. Первообразной для функции f называется такая функция F, производная которой равна данной функции.
2)Если F1 и F2 – две первообразные для одной и той же функции f, то они отличаются на постоянное слагаемое. ... Функция, производная которой тождественно равна нулю, является постоянной. Итак, F1 – F2 = С. Таким образом, все первообразные для функции f получаются из одной из них прибавлением к ней произвольной постоянной.
3)совокупность первообразных функции и называется непределенным интегралом от функции . Совокупность всех первообразных функции называется неопределенным интегралом от и обозначается символическим выражением , которое читается "интеграл от эф от икс по дэ икс".
4) Знак интеграла (∫) используется для обозначения интеграла в математике.
5)Множество всех первообразных F(x)+C функции f(x) называется неопределенным интегралом функции f(x) и обозначается . Символ называется интегралом, f(x) называется подынтегральной функцией, f(x)dx называется подынтегральным выражением, x называется переменной интегрирования.
6)Подынтегральное выражение представляет собой дифференциал функции f(x). Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.
7)Если – одна из первообразных некоторой функции , то совокупность всех первообразных этой функции можно представить в виде , где C – произвольная постоянная. Функция, имеющая первообразную в некотором промежутке, называется интегрируемой, а процедуру нахождения первообразной называют интегрированием этой функции.
8)Неопределенный интеграл его свойства. ... Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функции f(x) и обозначается как ∫f(x)dx. Таким образом, если F - некоторая частная первообразная, то справедливо выражение ∫f(x)dx=F(x)+C, где C - произвольная постоянная.
9)Метод интегрирования, при котором интеграл с тождественных преобразований подынтегральной функции и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.
10)Геометрически определённый интеграл выражает площадь «криволинейной трапеции», ограниченной графиком функции[⇨].
11)Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления. Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x).
12)Криволинейная трапеция – плоская фигура, ограниченная графиком неотрицательной непрерывной функции у = f(x), определенной на отрезке [a; b], осью абсцисс и прямыми х = а, х = b – см. рис.
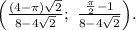
Объяснение:
Область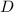 
, задающая плоскую фигуру, координаты центра тяжести которого требуется найти, задана такими кривыми:
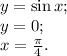
Известны ограничения сверху и снизу на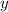 
, а для 
только сверху. Тогда ограничение снизу будет граничным с остальными:
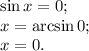
Получили четвёртое и последнее ограничение для области. Тогда область 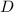задана такими кривыми:
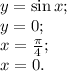
Переведём условия в вид неравенств:
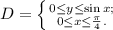
Поскольку левые части неравенств области нулевые, можем сразу вычислить площадь области, не используя двойной интеграл, а вместо него использовав одномерный определённый интеграл, в качестве функции использовав верхний предел 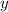, а в качестве пределов интегрирования — части неравенства для .
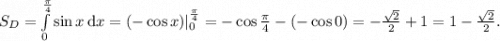
Как известно, если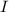 
— точка центра тяжести, то 
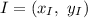, и они в свою очередь:
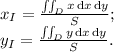
Найдём обе координаты точки центра тяжести.
Начнём с абсциссы:
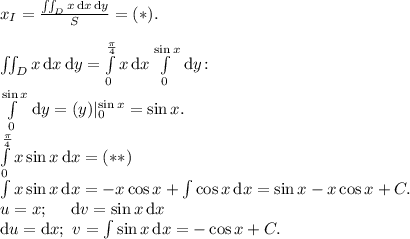
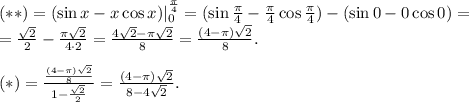
Теперь ордината:
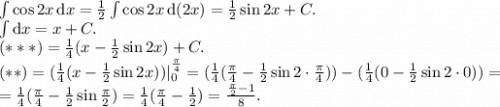
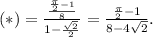
ответом будут найденные координаты,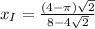 
и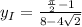 
.
S= 1*1=1см квадратных
2 дм= 20 см
S= 20*20= 400 см квадратных