25 (км/ч)
Объяснение:
Расстояние против течения - Sпр.теч. = 100 км
Время против течения - tпр.теч. = 4часа
Расстояние по течению - Sпо теч. = 150 км
Время по течению - tпо теч. = 5 часов
На сколько км/ч скорость течения реки меньше собственной скорости лодки?
Пусть Vc. - собственная скорость лодки, а Vт. - скорость течения реки.
⇒ Vпо теч.=Vс. + Vт., Vпр.теч. = Vс. - Vт.
Чтобы найти скорость, нужно расстояние разделить на время:
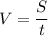
Найдем скорости по течению и против течения:
Vпр.теч. = 100:4 = 25 (км/ч)
Vпо теч. = 150:5 = 30 (км/ч)
Получим систему:
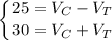
Сложим уравнения и найдем Vc.:
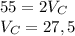
Собственная скорость лодки Vс.=27,5 км/ч
Найдем скорость течения реки:
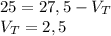(км/ч)
Найдем, на сколько км/ч скорость течения реки меньше собственной скорости лодки:
27,5 - 2,5 = 25 (км/ч)
1) Точки пересечения с осями.
- с осью Оу: х = 0, у =0^3+0^2-16*0-16 = -16, точка (0; -16).
- с осью Ох: у = 0.
x^3+x^2-16x-16 = 0.
Преобразуем заданное уравнение:
у =x^3+x^2-16x-16 = х²(х+1)-16(х+1) = (х²-16)(х+1) = (х-4)(х+4)(х+1).
у = 0, (х-4)(х+4)(х+1) = 0.
Отсюда получаем 3 корня уравнения: х₁ = 4, х = -4, х = -1.
2) Для того, чтобы найти экстремумы, нужно найти производную и приравнять её нулю и корни этого уравнения будут экстремумами данной функции:
y' = 3x² + 2 x - 16 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D=2^2-4*3*(-16)=4-4*3*(-16)=4-12*(-16)=4-(-12*16)=4-(-192)=4+192=196;
Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√196-2)/(2*3)=(14-2)/(2*3)=12/(2*3)=12/6=2;
x₂=(-√196-2)/(2*3)=(-14-2)/(2*3)=-16/(2*3)=-16/6=-(8/3) ≈ -2,6667.
Значит, экстремумы в точках:
((-8/3); (400/27)),
(2, -36).
3) Определяем минимумы и максимумы функции и промежутки знакопостоянства.
Для этого находим значения производной вблизи критических точек.
х = -3 -2.667 -2 1 2 3
у' = 5 0 -8 -11 0 17.
Где производная меняет знак с + на - там максимум функции ((х=(-8/3); у= (400/27)), а где меняет знак с - на + там минимум функции (х=2; у=-36)).
Функция возрастает на промежутках -∞ < x < (-8/3) и 2 < x < +∞,
а убывает на промежутке (-8/3) < x < 2.
4) Найдем точки перегибов, для этого надо решить уравнение
y'' = 0 (вторая производная равняется нулю), корни полученного уравнения будут точками перегибов для указанного графика функции,
х - 36+4х = 3х+2
Переносим Х в левую, остальные числа в правую части с противоположными знаками
х+4х-3х = 2+36
2х = 38
х = 19