Объяснение:Если y=f(u), где u=u(x), то есть y — сложная функция, то производная сложной функции находится по следующему правилу: y’=f'(u)·u'(x), то есть производную внешней функции f надо умножить на производную внутренней функции u. На первых порах нам разобраться, как находится производная сложной функции для каждой конкретной.
Если y=f(u), где u=u(x), то есть y — сложная функция, то производная сложной функции находится по следующему правилу: y’=f'(u)·u'(x), то есть производную внешней функции f надо умножить на производную внутренней функции u. На первых порах нам разобраться, как находится производная сложной функции для каждой конкретной.
1. Обратно пропорциональная зависимость :
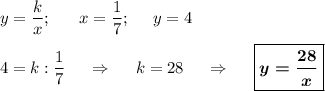
2. Решите графически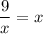 
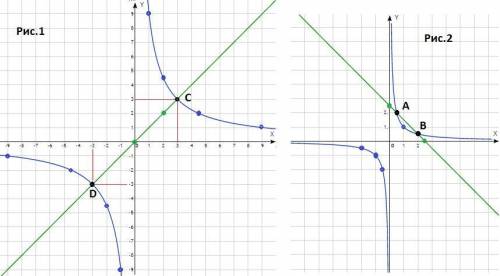
График функции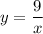 
- гипербола в первой и третьей четвертях (k=9>0). Точки для построения :
x -9 -4,5 -3 -2 -1 1 2 3 4,5 9
y -1 -2 -3 -4,5 -9 9 4,5 3 2 1
График функции y = x - прямая линия, проходящая через начало координат. Точки для построения
x 0 2
y 0 2
ответ : (-3; -3) и (3; 3) - рис. 1.
3. Графически, сколько решений имеет уравнение 
График функции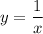 
- гипербола в первой и третьей четвертях (k=1>0). Точки для построения :
x -2 -1 -0,5 0,5 1 2
y -0,5 -1 -2 2 1 0,5
График функции y = 2,5 - x - прямая линия. Точки для построения
x 0 2,5
y 2,5 0
ответ : уравнение имеет 2 решения - рис. 2.
Yв=2,25-4,5+3=0,75
(-1,5;0,75)
2) Xв=3/2=1,5
Yв=2,25-4,5+3=0,75
(1,5;0,75)