Объяснение:
В первой системе очень удобно выразить х, и подставить во второе уравнение. После чего открываем скобки и приводим подобное.
Получаем квадратное уравнение, я умножила всё на -1 чтобы было удобнее.
Можно воспользоваться теоремой Виета, дискриминантом и т.д
Я для раскрытия квадратного многочлена использую такую формулу
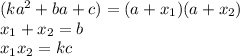
при этом, если k>0 уравнение следует записать в таком виде

и только потом выносить общий множитель за скобку.
В первом уравнении второй системы у нас разность квадрата, после того как мы нашли ее, можем возвести правую и левую части в корень, и извлечь его. После этого выражаем одну переменную через другую и ищем корни уравнения.


Объяснение:
В основе метода математической индукции (ММИ) лежит принцип математической индукции: утверждение $P(n)$ (где $n$ - натуральное число) справедливо при $\forall n \in N$, если:
Утверждение $P(n)$ справедливо при $n=1$.
Для $\forall k \in N$ из справедливости $P(k)$ следует справедливость $P(k+1)$.
Доказательство с метода математической индукции проводится в два этапа:
База индукции (базис индукции). Проверяется истинность утверждения при $n=1$ (или любом другом подходящем значении $n$)
Индуктивный переход (шаг индукции). Считая, что справедливо утверждение $P(k)$ при $n=k$, проверяется истинность утверждения $P(k+1)$ при $n=k+1$.
Метод математической индукции применяется в разных типах задач:
Доказательство делимости и кратности
Доказательство равенств и тождеств
Задачи с последовательностями
Доказательство неравенств
Нахождение суммы и произведения
5x+3y=1 (умножь на 5)
получается:
-21 х -15y=15
25x+15y=5
затем ты видишь что -15y и 15y самоуничтожаться,то есть будет
4x=20
x=5,ТОГДА подставим х под любое из 2 выражений(ответ будет один и тот же),вот выражение 25x=15y+5,подставляем получается:25*5+15y=5;125+15y=5;15y=5-125;15y-120;y=-8
надеюсь ты поняла как это делается