 0 не является
0 не является 0 не является
0 не является 0 не является
0 не является 0 не является
0 не является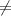 0 не является
0 не является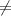 0 не является
0 не является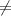 0 не является
0 не является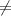 0 не является
0 не является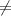 -11
-11
Объяснение:
1) log₂(x-1)=1
используем определение логарифма -
логарифмом числа b по основанию a ( logₐb ) называется такое число n, что b=aⁿ, у нас а =2, b = (x-1), n = 1 подставим наши значения
(х-1)=2¹ ⇒ х-1=2⇒х=3 отрезок (0;3]
2) log₂(x-1)≤0
по определению логарифма b >0, у нас х-1 > 0 ⇒ х > 1 это первое условие
ищем второе. сначала решаем уравнение log₂(x-1)=0
используем свойство логарифма logₐ1=0 имеем х-1 = 1 ⇒ х=2
на отрезке (1;2] проверим знак логарифма
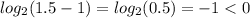
это наш отрезок (1;2]
3)
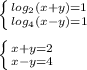
x=3; y=-1
4)
log₂(4-x)≤1
4-x>1 ⇒ x < 4
log₂(4-x)=1 ⇒ 2=4-x ⇒x=2
[2;4)
5)
log₇log₂log₇49
раскручиваем справа
log₇log₂log₇49=log₇log₂2=log₇1=0
log₁₂3+log₁₂4= log₁₂3*4=log₁₂12=1
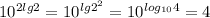
!x!=3
x=3
x=-3
x=0
x=5
x=-5
|X|=0
x=0
3.
3Проверте что число 10 является корнем уравнения |x|=x а,число -10 его корнем не является
!x!=x
!10!=10 да корень
!-10!=10<> нет не корень
акие из чисел 1,2,0,-1,-2 являются корнями уравнения
-
надо подставить в выражения
1 1-1-1-6=-7 нет
2 8-4-4-12=-12 нет
0 0-0-0-0=0 да
-1 -1-1-1+6=-3 нет
-2 -8-4-4+12=-4 нет
1 1+4+1-6=0 да
2 8+16+2-6=20 нет
0 0+0+0-6=-6 нет
-1 -1+4-1-6=-4 нет
-2 -8+16-2-6=0 да