Рассмотрим 3 случая: с отрицательной, нулевой и положительной правой частью.
1. Если , то есть .
Тогда предполагается, что модуль должен принимать значения, не большие некоторого отрицательного, то есть тоже отрицательные. Но модуль не может принимать отрицательных значений. Значит, в этом случае неравенство решений не имеет.
2. Если , то есть .
Получаем неравенство:
Поскольку модуль не принимает отрицательных значений, достаточно решить уравнение:
3. Если , то есть , то получаем неравенство с положительной правой частью:
Проведем отрезки OB и OC, как показано на рисунке. Расстоянием от точки до прямой является длина перпендикуляра, проведенного к прямой. Поэтому, OE перпендикулярен AB, а OF перпендикулярен CD. Точки E и F делят свои хорды пополам (по свойству хорды) Получается, что треугольники OEB и OCF - прямоугольные, EB=AB/2 и CF=CD/2. По теореме Пифагора: OB2=OE2+EB2 OB2=242+(20/2)2 OB2=576+100=676 OB=26 OB=OC=26 (т.к. OB и OC - радиусы окружности) По теореме Пифагора: OC2=CF2+FO2 OC2=(CD/2)2+FO2 262=(CD/2)2+102 676=(CD/2)2+100 (CD/2)2=576 CD/2=24 CD=48 ответ: CD=48
1) График функции Y=x^2+2x-3 - это парабола ветвями вверх. Область значень функції - все действительные числа (R).
2) Вершина параболы находится в точке х = -в / 2а = -2 / 2*1 = -1. у = (-1)² +2*(-1) - 3 = 1-2-3 = -4. Точки пересечения графика оси х соответствуют значению у = 0: x² + 2x - 3 = 0. Квадратное уравнение, решаем относительно x: Ищем дискриминант:D=2^2-4*1*(-3)=4-4*(-3)=4-(-4*3)=4-(-12)=4+12=16; Дискриминант больше 0, уравнение имеет 2 корня: x₁=(√16-2)/(2*1)=(4-2)/2=2/2=1; x₂=(-√16-2)/(2*1)=(-4-2)/2=-6/2=-3. Функція набуває додатних значень при x < -3 и x > 1.
Рассмотрим 3 случая: с отрицательной, нулевой и положительной правой частью.
1. Если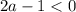 , то есть
, то есть 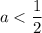 .
.
Тогда предполагается, что модуль должен принимать значения, не большие некоторого отрицательного, то есть тоже отрицательные. Но модуль не может принимать отрицательных значений. Значит, в этом случае неравенство решений не имеет.
2. Если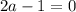 , то есть
, то есть 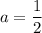 .
.
Получаем неравенство:
Поскольку модуль не принимает отрицательных значений, достаточно решить уравнение:
3. Если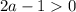 , то есть
, то есть 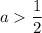 , то получаем неравенство с положительной правой частью:
, то получаем неравенство с положительной правой частью:
Заменим его следующим двойным неравенством:
Таким образом получаем ответ:
при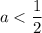 : решений нет
: решений нет
при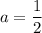 :
: 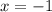
при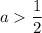 :
: ![x\in[-2a;\ 2a-2]](/tpl/images/2004/6663/9d563.png)