Напомним, что неравенства называются равносильными, если у них совпадают множества решений.
Решим первое неравенство. ОДЗ: x≥2. Если x=2, неравенство превращается в 0>0, поэтому x=2 не входит в ответ. Если x>2, корень из x-2 больше 0, поэтому он не влияет на знак левой части и может быть отброшен. Получается неравенство x-a>0; x>a. Остается пересечь условия x>2 и x>a. Если a<2, решениями первого неравенства служат все x>2, что не совпадает с множеством решений второго неравенства. Если же a≥2, решениями первого неравенства служат все x>a, что совпадает с множеством решений второго неравенства.
Вывод: неравенства равносильны при a≥2
а) xp < yp
б) xp > yp
в) 1/x > 1/y
г) 1/x < 1/y
Объяснение:
а) Представь, что у тебя x = 1, а y = 2. P = любому положительному числу. Для наглядности возьмём 1.
Если ты умножишь x на p, то получишь 1 * 1 = 1. Если y умножишь на p, то получишь 2 * 1 = 2. Следовательно, у тебя произведение x и p будет меньше, чем y и p. Т.к изначально известно, что x < y.
б) Продолжаю объяснение из а. X и Y оставляем такими же: x = 1, y = 2. Однако если p - любое отрицательное число, то произведение x и p будет больше, чем y и p. Допустим, в этом примере p у нас будет = -1
Тогда получим x * p = 1 * (-1) = -1, а y * p = 2 * (-1) = -2. Тут не так определяется величина числа, как с положительными числами. В случае с отрицательными числами, больше будет то число, которое ближе к нулю. В данном примере ближе к нулю будет -1.
в) Чем меньше число на которое ты делишь, тем больше получается значение. К примеру, пусть x = 2, а y = 4. Тогда получим :
1/x = 1/2 = 0,5
1/y = 1/4 = 0,25
г) Пусть x = -2, а y = -4. тогда:
1 / (-2) = -0,5
1 / (-4) = -0,25
-0,25 > -0,5 т.к ближе к нулю.
у=2 у=5
Объяснение:
х+2х+5=у -х+2х+5=у
3х+5=у х+5=у
Эти два графика (3х+5=у и х+5=у ) - прямые
уравнение прямой - кх+в
т.к к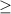
0 и в 
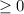во всех случаях, то график будет иметь вид (см картинку)
тогда просто подставляем -3 и 0 т.к. это наименьшее и наибольшее значения
у(-3)=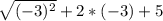
= 2
у(0)=
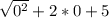=5