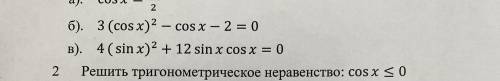
Чтобы сравнить числовые выражения (√6 + √10) и (3 + √7), возведем оба выражения в квадрат.
(√6 + √10)^2 = (√6)^2 + 2√6√10 + (√10)^2 = 6 + 2√60 + 10 = 16 + 4√15;
(3 + √7)^2 = 3^2 + 2 * 3√7 + (√7)^2 = 9 + 6√7 + 7 = 16 + 6√7.
В выражениях 16 + 4√15 и 16 + 6√7 первые слагаемые равны, поэтому надо сравнить вторые слагаемые. Возведем их во вторую степень.
(4√15)^2 = 16 * 15 = 240;
(6√7)^2 = 36 * 7 = 252.
240 < 252, значит 4√15 < 6√7, поэтому (16 + 4√15) < (16 + 6√7), следовательно (√6 + √10) < (3 + √7).
Объяснение:
1 . б) 3(cosx)² - cosx - 2 = 0 ; gffgrthtyu76788786
заміна t = cosx , | t | ≤ 1` ;
3t² - t - 2 = 0 ; D = 25 > 0 ; t = - 2/3 ; t = 1 ;
cosx = 1 ; або cosx = - 2/3 ;
x = 2πn , nЄ Z ; x = ± ( π - arccos2/3 ) + 2πn , nЄ Z .
В - дь : x = 2πn , nЄ Z ; x = ± ( π - arccos2/3 ) + 2πn , nЄ Z .
в) 4(sinx)² + 12sinxcosx = 0 ;
4sinx(sinx + 3cosx ) = 0 ;
sinx = 0 ; або sinx + 3cosx = 0 ;
x = πn , nЄ Z ; sinx = - 3cosx ; │: cosx ≠ 0
tgx = - 3 ;
x = - arctg3 + πn , nЄ Z .
В - дь : x = πn , nЄ Z ; x = - arctg3 + πn , nЄ Z .