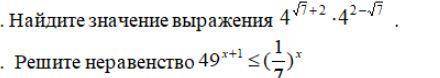
Начнем с первого пункта.
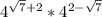
Так как основания одинаковы (равны 4), мы можем упростить по формуле:
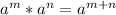 , где (в нашем случае) a = 4, m =
, где (в нашем случае) a = 4, m = 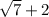 , n = 2-
, n = 2-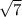
Подставляем.
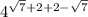 =
= 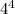 , что равно 256.
, что равно 256.
Пункт второй.
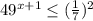
В данном случае нужно самому привести к общему основанию.
49 - это 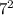 , а
, а  - это
- это 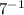 .
.
Значит,
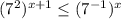

А вот тут, так как это неравенство, где основания уже одинаковы, т.е. равны 7, мы можем убрать основания, оставив только степени. Опять же, это можно делать только если основания одинаковы.
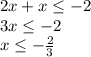
Заметим ,что наименьшие значения функций:
2^(x-3) +4>4
5*|tg(x)|+3*|ctg(x)|>=2√15 (из соображений полного квадрата и положительности каждого из членов |tg(x)|*|ctg(x)|=1)
Рассмотрим случай когда : a<-2√15
В этом случае числитель будет отрицателен при любом x:
a-(2^(x-3) +4)<0
Знаменатель же ,будет положителен не всегда, тк при каком нибудь x обязательно найдется значение 5*|tg(x)|+3*|ctg(x)|>a ,тк оно имеет область значений от 2√15 до бесконечности) . То есть в зависимости от x, может быть как и положителен так и отрицателен. Вывод: при a<-2√15 будут существовать решения неравенства.
Рассмотрим случай когда: a>4
Тут ситуация иная:
Знаменатель тут всегда положителен,а вот числитель не всегда отрицателен,то есть решения так же будут существовать .
Наконец рассмотрим случай когда:
-2√15<=a<=4
В этом случае числитель всегда отрицателен (при любом x), а знаменатель же наоборот будет неотрицателен. Таким образом только на этом интервале неравенство не будет иметь решения не для какого x. Тк отношение числителя и знаменателя всегда будет отрицательным. P.S Не у кого тут нет вопросов почему строгое неравенство для -2√15(знаменателю быть равным нулю не запрещается,тк наша цель отсутствие решений). Почему же строгое и для 4, а дело все в том ,что: 2^(x-3) +4≠4 , а только стремится к нему при стремлении x к бесконечности,поэтому опасаться за равенство нулю числителя не стоит.
Таким образом
ответ: a∈[-2√15;4]
Отметьте лучшим решением и поставьте сердечко