Данную систему попробую решить чисто аналитически. Редко так деляю, поэтому надеюсь, что ничего не потеряю.
Рассмотрим первую строку системы:
Заметим, что при она теряет смысл.
Действительно: , неверно.
Выразим из рассматриваемого уравнения :
Подставим полученную фразу во вторую строку системы:
Упростим ее:
ОДЗ для данной дроби .
Помня это, перейдем к более комфортной записи:
При уравнение перестает быть квадратным. Это означает, что если мы получим x, не равный 5, то такое значение параметра нужно взять в ответ.
Значит является фрагментом ответа.
При найденном вычислим :
Итого при система имеет единственное решение .
При имеем параболу. Чтобы квадратное уравнение имело один единственный корень, нужно, чтобы его дискриминант был равен 0 (естественно, важно, чтобы тогда корень не был равен 5). В нашем случае еще допустимо, чтобы уравнение имело два корня, один из которых равен 5, так как по ОДЗ он не подойдет и в итоге из двух останется один.
Рассчитаем дискриминант, деленный на четыре (для более простого счета; можно считать обычный):
Приравняем его к нулю:
При исходная система уравнений имеет единственное решение . Берем его в ответ.
Подставим теперь в наше уравнение:
При исходная система уравнений имеет единственное решение . Такое значение параметра подходит.
Итого:
При система имеет единственное решение При исходная система уравнений имеет единственное решение При исходная система уравнений имеет единственное решение
2) {3x+4y=-1 Тут всё нужно умножить на -2, чтобы потом избавиться от x 2x+5y=4 Тут всё нужно умножить на 3, чтобы потом избавиться от X АНАЛОГИЧНО ПЕРВОМУ: {-6x-8y=2 6x+15y=12
Ход решения неравенства на фото : Как решать неравенства 1)приравниваем данное выражение(уравнение) к нулю 2)дальше решаем это уравнение 3)получается корни (точки) 4)строим луч на нем обозначает точку(точки) если несколько ,то сначала меньшее число пишем слева,потом большее 5)определяем знак больше большего числа(например больший корень 8,значит берем х=9,и подставляем в данное уравнение Если положительное число то ставим +,а дальше чередуем +,-,+ или -,+,- 6)смотрим по неравенству какой ответ надо выбирать Если в неравенстве >,то где стоит +,если<,то где стоит минус
(см. объяснение)
Объяснение:
Данную систему попробую решить чисто аналитически. Редко так деляю, поэтому надеюсь, что ничего не потеряю.
Рассмотрим первую строку системы:
Заметим, что при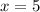 она теряет смысл.
она теряет смысл.
Действительно: , неверно.
, неверно.
Выразим из рассматриваемого уравнения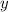 :
:
Подставим полученную фразу во вторую строку системы:
Упростим ее:
ОДЗ для данной дроби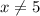 .
.
Помня это, перейдем к более комфортной записи:
При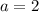 уравнение перестает быть квадратным. Это означает, что если мы получим x, не равный 5, то такое значение параметра нужно взять в ответ.
уравнение перестает быть квадратным. Это означает, что если мы получим x, не равный 5, то такое значение параметра нужно взять в ответ.
Значит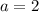 является фрагментом ответа.
является фрагментом ответа.
При найденном вычислим
вычислим 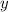 :
:
Итого при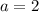 система имеет единственное решение
система имеет единственное решение 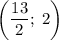 .
.
При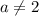 имеем параболу. Чтобы квадратное уравнение имело один единственный корень, нужно, чтобы его дискриминант был равен 0 (естественно, важно, чтобы тогда корень не был равен 5). В нашем случае еще допустимо, чтобы уравнение имело два корня, один из которых равен 5, так как по ОДЗ он не подойдет и в итоге из двух останется один.
имеем параболу. Чтобы квадратное уравнение имело один единственный корень, нужно, чтобы его дискриминант был равен 0 (естественно, важно, чтобы тогда корень не был равен 5). В нашем случае еще допустимо, чтобы уравнение имело два корня, один из которых равен 5, так как по ОДЗ он не подойдет и в итоге из двух останется один.
Рассчитаем дискриминант, деленный на четыре (для более простого счета; можно считать обычный):
Приравняем его к нулю:
При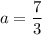 исходная система уравнений имеет единственное решение
исходная система уравнений имеет единственное решение 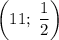 . Берем его в ответ.
. Берем его в ответ.
Подставим теперь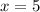 в наше уравнение:
в наше уравнение:
При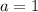 исходная система уравнений имеет единственное решение
исходная система уравнений имеет единственное решение  . Такое значение параметра подходит.
. Такое значение параметра подходит.
Итого:
ПриЗадание выполнено!