Расстояние между пристанями а и в по течению реки равно 84 км. из пристани в вниз по течению отправился плот. одновременно из пристани а вдогонку за плотом отправился катер,собственная скорость 21 км/ч. через сколько часов катер нагонит плот,если известно, что скорость течения реки равна 3 км/ч

👇

Увидеть ответ

Ответ:

bellalove200

21.01.2023

1)21+3-3=21-скорость сближения
2)84/21=4ч

4,8(20 оценок)

Открыть все ответы

Ответ:

evelinastepenko

21.01.2023

По определению
$|x|= \left \{ {{x, x \geq 0} \atop {-x,x$
Поэтому
$|x-2|= \left \{ {{x-2,x-2 \geq 0} \atop {-x+2,x-2$
т.е
слева от точки 2 подмодульное   справа от точки 2 подмодульное
выражение берется со знаком "-"       выражение со знаком "+"
   -     +
--------------------------------------------------------(2)------------------
Аналогично
$|x-4|= \left \{ {{x-4,x-4 \geq 0} \atop {-x+4,x-4$
т.е
слева от точки 4 подмодульное      справа от точки 4 подмодульное
выражение берется со знаком "-" выражение со знаком "+"
------------------------------------------------------------------(4)------------------
   - +
Изобразим на одной координатной прямой. Причем знаки первого подмодульного выражения будем изображать наверху, знаки второго - внизу
   - + +
--------------------------------------(2)--------------------(4)--------------
   -    - +
Раскрываем модули на (-∞;2].
Оба подмодульных выражения раскрываем с противоположным знаком:   |x-2|=-(x-2)=-х+2 ;   |x-4|=-(x-4)=-х+4
Уравнение принимает вид:
-x+2-x+4=3
-2х+6=3
-2х=-3
х=3/2
х=1,5
1,5 ∈(-∞;2]

Раскрываем модули на (-2;4]: |x-2|=x-2 ;   |x-4|=-(x-4)=-х+4
Уравнение принимает вид:
x-2-x+4=3
2=3 -неверное равенство
Уравнение не имеет корней

Раскрываем модули на (4;+∞).
Оба подмодульных выражения раскрываем не меняют выражения:
|x-2|=x-2 ;   |x-4|=x-4
Уравнение принимает вид:
x-2+x-4=3
2х-6=3
2х=9
х=9/2
х=4,5
4,5 ∈(4;+∞)
ответ. 1,5 ; 4,5
Остальные примеры решаются аналогично.
2)
   - + +
-----------(-2)-------------(3)------------
   + + -
на (-∞;-2] уравнение принимает вид: -х+2-3(3-х)+х=0 или 3х=7 х= 7/3 - не принадлежит промежутку (-∞;-2), не является корнем уравнения
на (2;3]   уравнение принимает вид: х-2-3(3-х)+х=0 или 5х=11   или    х=2,2
2,2∈ (2;3] , значит х=2,2 - корень уравнения
на (3;+∞) уравнение принимает вид х-2+3(3-х)+х=0 или х=7
7∈(3;+∞), значит х=7 является корнем уравнения
ответ. 2,2 ; 7
3)
-    +    +
------------------(1)--------------------(4)----------------
   + + -

на (-∞;1] уравнение принимает вид: 4-х-2х+2=5-2х или х=1
1∈(-∞;1] , значит х=1 - корень уравнения.
на (1;4) уравнение принимает вид: 4-х+2х-2=5-2х или 3х=3 или х=1
1∉(1;4) , на данном промежутке уравнение не имеет корней
на (4;+∞) уравнение принимает вид: -4+х+2х-2=5-2х или 5х=11 или х=2,2
2,2∉(4;+∞) уравнение не имеет корней на данном промежутке
ответ. х=1
5)
|x| - - + +
|3x+2| - + + +
|2x-1|    - - - +
   ------------------(-2/3)-------(0)------------(1/2)---------------
(-∞;-2/3] - x -3x - 2 - 2x +1 = 5 или -6х=6 или х=-1
-1∈(-∞;-2/3] х=-1 - корень уравнения
(-2/3;0]    х - 3х - 2 - 2х + 1 = 5 или -4х=6 или    х=-3/2
-3/2∉(-2/3;0] х=-1,5 не является корнем уравнения
(0;1/2] x+3x+2-2x+1=5 или 2х=2 или х=1
1∉(0;1/2] х=1 не является корнем уравнения
(1/2;+∞) х+3х+2+2х-1=5 или 6х=4 х= 2/3
2/3∈(1/2;+∞)
ответ. х=-1 ; х=2/3

4,6(61 оценок)

Ответ:

Xzxzxzxzxzzxzxz

21.01.2023

Уравнение четвёртой степени имеет вид:
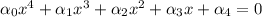
$\alpha _0x^4+ \alpha _1x^3+ \alpha _2x^2+ \alpha _3x+ \alpha _4=0$
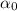Разделим обе части на коэффициент $\alpha _0$ , получаем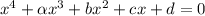
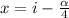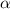$x^4+ \alpha x^3+ bx^2+cx+d=0$
где a, b, c, d – произвольные вещественные числа.

Уравнения вида приводится уравнение четвёртой степени, у которых отсувствует третьей степени., поэтому нужно сделать замену переменных, тоесть
$x=i- \frac{ \alpha }{4}$ , где $\alpha$ - коэффициент перед х^3 и 4 - произвольные вещественные числа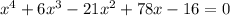

В нашем случае такое уравнение: x^4+6x^3-21x^2+78x-16=0

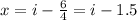Заменим $x=i- \frac{6}{4} =i-1.5$ , получаем
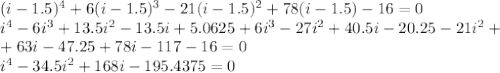
$(i-1.5)^4+6(i-1.5)^3-21(i-1.5)^2+78(i-1.5)-16=0\\ i^4-6i^3+13.5i^2-13.5i+5.0625+6i^3-27i^2+40.5i-20.25-21i^2+\\+63i-47.25+78i-117-16=0\\ i^4-34.5i^2+168i-195.4375=0$

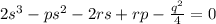
Получаем кубическое уравнение: $2s^3-ps^2-2rs+rp- \frac{q^2}{4}=0$
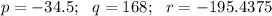
В нашем случае: $p=-34.5;\,\,\,\,q=168;\,\,\,\,r=-195.4375$
Подставляем и получаем уравнение
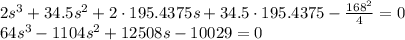
$2s^3+34.5s^2+2\cdot195.4375s+34.5\cdot195.4375- \frac{168^2}{4}=0\\ 64s^3-1104s^2+12508s-10029=0$
Разложим одночлены в сумму нескольких
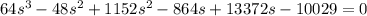
64s^3-48s^2+1152s^2-864s+13372s-10029=0

Выносим общий множитель
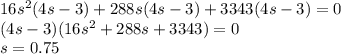
$16s^2(4s-3)+288s(4s-3)+3343(4s-3)=0\\ (4s-3)(16s^2+288s+3343)=0\\ s=0.75$
Уравнение 16s²+288s+3343=0 решений не имеет, так как D<0

Таким образом для решения уравнения остается квадратное уравнение
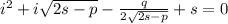
$i^2+i \sqrt{2s-p} - \frac{q}{2\sqrt{2s-p}}+s=0$
Заменяем
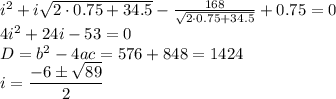
$i^2+i\sqrt{2\cdot0.75+34.5}- \frac{168}{\sqrt{2\cdot0.75+34.5}} +0.75=0\\ 4i^2+24i-53=0\\ D=b^2-4ac=576+848=1424\\ i= \dfrac{-6\pm \sqrt{89} }{2}$

Возвращаемся к замене
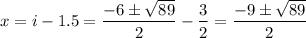
$x=i-1.5=\dfrac{-6\pm \sqrt{89} }{2}- \dfrac{3}{2} =\dfrac{-9\pm \sqrt{89} }{2}$

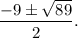
Окончательный ответ: $\dfrac{-9\pm \sqrt{89} }{2}.$