
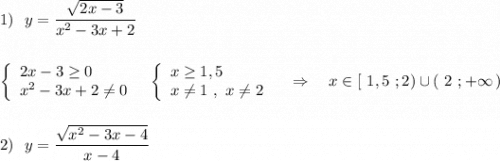
![\left\{\begin{array}{l}x^2-3x-4\geq 0\\x-4\ne 0\end{array}\right\ \ \left\{\begin{array}{l}(x+1)(x-4)\geq 0\\x\ne 4\end{array}\right\ \ \left\{\begin{array}{l}x\in (-\infty ;-1\ ]\cup [\ 4\ ;+\infty )\\x\ne 4\end{array}\right\\\\\\x\in x\in (-\infty ;-1\ ]\cup (\ 4\ ;+\infty )](/tpl/images/2009/2878/b6112.png)
![3)\ \ y=\dfrac{\sqrt{9-x^2}}{2x-1}\\\\\\\left\{\begin{array}{l}9-x^2\geq 0\\2x-1\ne 0\end{array}\right\ \ \left\{\begin{array}{l}(3-x)(3+x)\geq 0\\x\ne 0,5\end{array}\right\ \ \left\{\begin{array}{l}(x-3)(3+x)\leq 0\\x\ne 0,5\end{array}\right\\\\\\\left\{\begin{array}{l}x\in [-3\ ;\ 3\ ]\\x\ne 0,5\end{array}\right\ \ \ \Rightarrow \ \ \ x\in [-3\ ;0,5\ )\cup (\ 0,5\ ;\ 3\ ]](/tpl/images/2009/2878/95193.png)
![4)\ \ y=\dfrac{\sqrt{x^2-x-6}}{x-7}\\\\\\\left\{\begin{array}{l}x^2-x-6\geq 0\\x-7\ne 0\end{array}\right\ \ \left\{\begin{array}{l}(x+2)(x-3)\geq 0\\x\ne 7\end{array}\right\ \ \left\{\begin{array}{l}x\in (-\infty ;-2\ ]\cup [\ 3\ ;+\infty )\\x\ne 7\end{array}\right\\\\\\x\in (-\infty ;-2\ ]\cup [\ 3\ ;\ 7\ )\cup (\ 7\ ;+\infty )](/tpl/images/2009/2878/100e6.png)
Методика знаходження області визначення для всіх функцій одна і та ж: потрібно виявити точки при яких функція не існує, а потім виключити їх з множини дійсних чисел R. В результати отримаємо набір проміжків чи інтервалів або точки, які і утворюють область визначення. У даному випадку необхідно використати лише наступні правила:
знаменник дробу не може дорівнювати;підкореневий вираз не може бути меншим 0.
![\\y=\frac{\sqrt{x^2-3x-4}}{x-4}\\\left \{ {{x^2-3x-4\geq 0} \atop {x-4\neq 0}} \right. \\\left \{ {{(x-4)(x+1)\geq 0} \atop {x\neq 4}} \right. \\\\D=(-\infty; -1]U(4; \infty)](/tpl/images/2009/2878/d8d2d.png)
![\\y=\frac{\sqrt{9-x^2}}{2x-1}\\\left \{ {{9-x^2\geq 0} \atop {2x-1\neq 0}} \right\\\left \{ {{(3-x)(3+x)\geq 0} \atop {2x\neq 1}} \right\\\left \{ {{(3-x)(3+x)\geq 0} \atop {x\neq 0,5}} \right\\D=[-3; 0,5)U(0,5; 3]](/tpl/images/2009/2878/3bd8f.png)
![y=\frac{\sqrt{x^2-x-6} }{x-7} \\\left \{ {{x^2-x-6\geq 0} \atop {x-7\neq 0}} \right. \\\lef\{ {{(x+2)(x-3)\geq 0} \atop {x\neq 7}} \right. \\\\D=(-\infty; -2] U [3; 7) U (7;\infty)](/tpl/images/2009/2878/82fb6.png)
![1. найдите наибольшее и наименьшее значение функции : f(x) = - на промежутке [0; 3] 2. тело движется](/tpl/images/0197/9921/5115d.jpg)