Question

Дошёл до следующего: a + b = 0;
a = -b;
f(0)=f(-b)*f(b)
Но не могу понять, какое значеие будет у этого произведения (1 или -1). Оттуда отношение уже не сложно вывести.

Answer 1

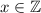Пусть $x\in\mathbb{Z}$, тогда по свойству функции будет верно, что $f(x)=f(0+x)=f(0)\cdot f(x)\iff f(x)\cdot\Big(1-f(0)\Big)=0$.

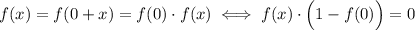Поскольку по условию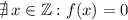 $\nexists\,x\in\mathbb{Z}:f(x)=0$, то получаем, что $f(0)=1$.

Отсюда получаем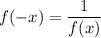 $f(-x)=\dfrac{1}{f(x)}$.