
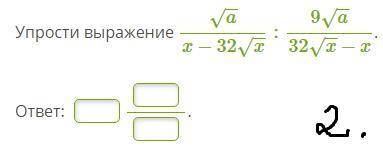
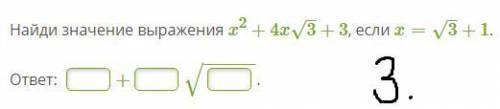
1 неравенство - вся числ. прямая
2 неравенство - не имеет решений
3 неравенство - открытый промежуток
4 неравенство - объединение двух промеж
Объяснение:
ax²+bх+c ≥ 0
ах²+bх+с ≤ 0
D = b²-4ас
Если D<0, но при этом a>0 и само неравенство > 0 => его решение - вся числовая прямая
Если D<0, но при этом a<0, и само неравенство ≥ 0 => оно не имеет решений
Если D>0, но при этом a>0 и само неравенство < 0 => решение - открытый промежуток
Если D>0, но при этом а<0 и само неравенство <0 => решение - объединение двух промежутков
а) х²=у≥0, тогда у²-8у+7=0, по Виету у=1; у=7, Вернемся к х,
х²=7⇒х=±√7; х²=1⇒х=±1
ответ х=±√7; х=±1
б) (х²-5х+4)(х²-5х+1)=28; х²-5х+1=у, тогда ( у+3)*у=28; у²+3у-28=0; по Виету у=-7; у=4, возвратимся к х, получим х²-5х+1=-7; х²-5х+8=0, дискриминант равен 25-32=-7- корней нет. х²-5х+1=4; х²-5х-3=0;х=(5±√(25+12)/2=
(5±√37)/2
ответ (5±√37)/2
в) о.з.=х*(х+1)*(х-1)≠0, ⇒х≠0; х≠±1;
(3х-5)*х+(6х-5)*(х+1)=(3х+2)*(х-1);
3х²-5х+6х²+6х-5х-5=3х²-3х+2х-2;
6х²-3х-3=0; 2х²-х-1=0; по Виету х=-1/2; х=1- не входит в ОДЗ уравнения.
ответ х=-1/2
1)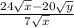
2)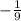
3)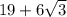
Объяснение:
1) знаменатели дробей одинаковые, значит можно записать дробь под одной чертой:
Приводим подобные слагаемые:
2) записываем дроби под одной чертой, перевернув их и заменив знак деления на умножение:
Нам ничего не мешает избавится от , так как он есть и в числителе и в знаменателе:
, так как он есть и в числителе и в знаменателе:
В знаменателе внутри скобок можно поменять слагаемые местами, вынеся минус:
3) подставляем в выражение вместо переменной её значение:
Раскрываем скобки:
Приводим подобные слагаемые: