ответ.

a) Уравнение оси ОХ: у=0 . Найдём точки пересечения графика функции с осью ОУ, для этого придадим значение х=0 и подставим в формулу .
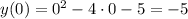
Точка пересечения графика с ОУ - точка А(0; -5) .
б) Найдём точки пересечения графика функции с осью ОХ, для этого надо придать значение у=0.
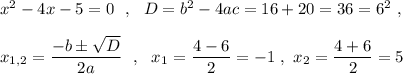
Точки пересечения графика с ОХ - точки В(1-;0) и С(5;0) .
в) Ось симметрии заданной параболы проходит через её вершину перпендикулярно оси ОХ . Найдём абсциссу вершины параболы.
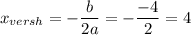
Ось симметрии - прямая х=2 .
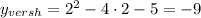 , координаты вершины параболы V(2;-9) .
, координаты вершины параболы V(2;-9) .
c) Для построения графика, можно найти координаты точки, симметричной точке А(0;-5) относительно оси х=4. Это точка D(4;-5) .
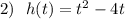
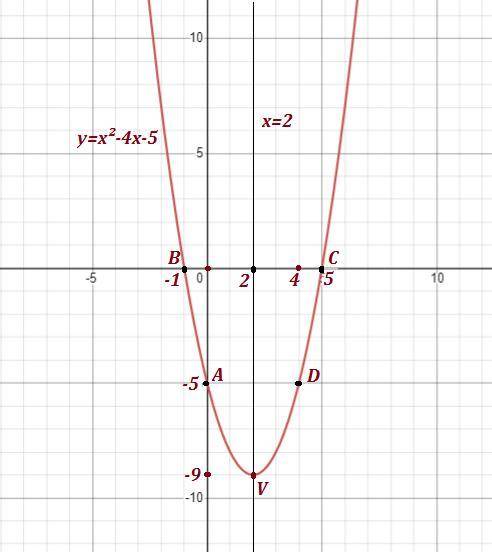
Графиком заданной функции является парабола с ветвями , направленными вверх, так как коэффициент перед t² равен 1>0 . А если ветви у параболы направлены вверх, то такая траектория движения не соответствует движению подброшенного мяча . Поэтому условие задано некорректно , с ошибкой .
Пусть сторона квадрата х см, тогда длина прямоугольника (3х) см, а ширина прямоугольника - (х - 5) см.
Т.к. площадь квадрата находят по формуле S = а², где а - сторона квадрата, о площадь данного квадрата равна (х²) см².
А т.к площадь прямоугольника находят по формуле S = a · b, где a и b - длина и ширина прямоугольника, то площадь данного прямоугольника будет равна S = 3х · (х - 5) = 3х² - 15х (см²).
Т.к. площадь квадрата на 50 см² меньше площади прямоугольника, то составим и решим уравнение:
3x² - 15х = x² + 50,
3x² - x² - 15x - 50 = 0,
2x² - 15x - 50 = 0,
D = (-15)² - 4 · 2 · (-50) = 225 + 400 = 625 ; √625 = 25,
x₁ = (15 + 25)/(2 · 2) = 40/4 = 10,
x₂ = (15 - 25)/(2 · 2) = -10·/4 = -2,5 - не подходит по условию задачи.
Значит, сторона квадрата равна 10 см.
ответ: 10 см.