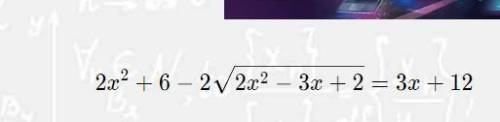
Количество игр: 2
:
Выигрыш (В) - 3 очка
Ничья (Н) - 1 очко
Проигрыш (П) - 0 очков
P(Н) = 0,1
Так как общая вероятность равна 1 или 100%, то:
P(В+П) = 1 - 0,1 = 0,9
По условию Р(В) = Р(П), тогда:
Р(В) = P(В+П) /2 = 0,9 / 2 = 0, 45
Р(П) = P(В+П) /2 = 0,9 / 2 = 0, 45
Команде не удасться выйти в следующий круг соревнований при следующих событиях:
1 игра - проигрыш, 2 игра - выигрыш1 игра - выигрыш, 2 игра - проигрыш1 игра - проигрыш, 2 игра - проигрыш1 игра - ничья, 2 игра - ничья1 игра - ничья, 2 игра - проигрыш1 игра - проигрыш, 2 игра - ничьяР(1) = Р(П) * Р(В) = 0,45 * 0,45 = 0,2025
Р(2) = Р(В) * Р(П) = 0,45 * 0,45 = 0,2025
Р(3) = Р(П) * Р(П) = 0,45 * 0,45 = 0,2025
Р(4) = Р(Н) * Р(Н) = 0,1 * 0,1 = 0,01
Р(5) = Р(Н) * Р(П) = 0,1 * 0,45 = 0,045
Р(6) = Р(П) * Р(Н) = 0,45 * 0,1 = 0,045
Вероятность того, что команде не удастся выйти в следующий круг соревнований:
Р = Р(1) + Р(2) + Р(3) + Р(4) + Р(5) + Р(6) = 0,2025 + 0,2025 + 0,2025 + 0,01 + 0,045 + 0,045 = 0,7075 = 0,71
2x² + 6 - 2√(2x² - 3x + 2) = 3x + 12
одз 2x² - 3x + 2 ≥ 0
D = 9 - 4*2*2 < 0
x ∈ R
2x² - 3x + 2 - 2√(2x² - 3x + 2) + 1 = 9
√(2x² - 3x + 2) = y > 0
y² - 2y + 1 = 9
(y - 1)² = 9
|y - 1| =3
1. y - 1 = 3
y = 4
√(2x² - 3x + 2) = 4
2x² - 3x + 2 = 16
2x² - 3x - 14 = 0
D = 9 + 4*2*14 = 121
x₁₂ = (3 +- 11)/4 = -2 7/2
2. y - 1 = -3
y = -2 < 0 нет решений
ответ 7/2, -2