х=-1
Объяснение:
Пусть y = uv, тогда y' = u'v + uv':
Решим левый интеграл:
cosx = \frac{1-t^2}{1+t^2} => dx = \frac{2}{1+t^2}dt\\ \int \frac{2(1+t^2)}{(1+t^2)(1-t^2)} dt = \int \frac{2}{(1-t)(1+t)}dt = \int ( \frac{1}{1-t} + \frac{1}{1+t})dt = ln(1-t)+ln( 1+t) = ln|1-t^2| = ln|1-tg^2\frac{x}{2}| \\" class="latex-formula" id="TexFormula2" src="https://tex.z-dn.net/?f=%5Cint%20%5Cfrac%7Bdx%7D%7Bcosx%7D%3B%5C%5C%20tg%5Cfrac%7Bx%7D%7B2%7D%3Dt%20%3D%3E%20cosx%20%3D%20%5Cfrac%7B1-t%5E2%7D%7B1%2Bt%5E2%7D%20%3D%3E%20dx%20%3D%20%5Cfrac%7B2%7D%7B1%2Bt%5E2%7Ddt%5C%5C%20%20%5Cint%20%5Cfrac%7B2%281%2Bt%5E2%29%7D%7B%281%2Bt%5E2%29%281-t%5E2%29%7D%20dt%20%3D%20%5Cint%20%5Cfrac%7B2%7D%7B%281-t%29%281%2Bt%29%7Ddt%20%3D%20%5Cint%20%28%20%5Cfrac%7B1%7D%7B1-t%7D%20%2B%20%5Cfrac%7B1%7D%7B1%2Bt%7D%29dt%20%3D%20ln%281-t%29%2Bln%28%201%2Bt%29%20%3D%20ln%7C1-t%5E2%7C%20%3D%20ln%7C1-tg%5E2%5Cfrac%7Bx%7D%7B2%7D%7C%20%20%5C%5C" title="\int \frac{dx}{cosx};\\ tg\frac{x}{2}=t => cosx = \frac{1-t^2}{1+t^2} => dx = \frac{2}{1+t^2}dt\\ \int \frac{2(1+t^2)}{(1+t^2)(1-t^2)} dt = \int \frac{2}{(1-t)(1+t)}dt = \int ( \frac{1}{1-t} + \frac{1}{1+t})dt = ln(1-t)+ln( 1+t) = ln|1-t^2| = ln|1-tg^2\frac{x}{2}| \\">
Возвращаемся к исходному:
и 
Объяснение:
Первый модуль обращается в ноль при x=-2, второй - при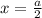 
.
Пусть сначала
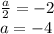
Тогда уравнение принимает вид 
и, очевидно, не имеет решений.
Пусть теперь
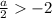
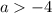
Если 
, то оба модуля раскрываются с плюсом и уравнение принимает вид:
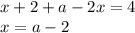
Полученный x будет корнем уравнения, если он принадлежит рассматриваемому отрезку, то есть если 
удовлетворяет системе неравенств
Решение системы: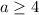 
Если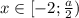 
, то уравнение принимает вид
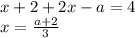
Полученный x будет корнем уравнения, если удовлетворяет системе:
Решение системы: 
Пусть, наконец,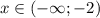 
. Тогда уравнение принимает вид
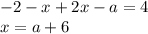
Полученный x будет корнем уравнения, если удовлетворяет системе:
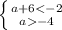
Эта система не имеет решений.
Теперь пусть 
, то есть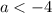 
.
Если 
, то
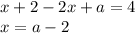
Система:
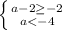
Нет решений.
Если 
, то
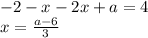
Система:
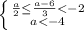
Решение системы: 
И наконец, если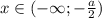 
, то
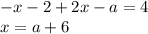
Система:
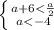
Решение: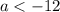 
Из вышесказанного очевидно, что
При 
- два решения
При - одно решение
При 
- нет решений
При 
- нет решений
При - одно решение
При 
- два решения
Таким образом, уравнение имеет одно решение при и
x³+x²-4x+2=0
x³+x² = x⁵
-4x+2 = 6x
x⁵-6x= -1
x= -1