Решите номер 33(4) Очень выручите

Question

Алгебра: Решите номер 33(4) Очень выручите

hahagnom · Accepted Answer

Пусть x - скорость первого автобуса, (x-4) - скорость второго автобуса. Тогда время, которое провел в пути первый автобус 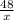$\frac{48}{x}$ , а время, которое провел в пути второй автобус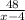 $\frac{48}{x-4}$

Из условия задачи

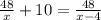
$\frac{48}{x}+10=\frac{48}{x-4}$

Решаем:

$\frac{48+10x}{x}=\frac{48}{x-4}$

48x+10x^2-192-40x=48x

10x^2-40x-192=0

5x^2-20x-96=0

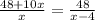
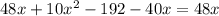
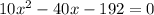
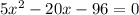
Решаем квадратное уравнение, находим дискриминант:

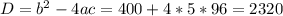
D=b^2-4ac=400+4*5*96=2320

Находим корни квадратного уравнения:

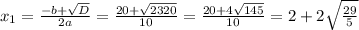
$x_1=\frac{-b+\sqrt{D}}{2a}=\frac{20+\sqrt{2320}}{10}=\frac{20+4\sqrt{145}}{10}=2+2\sqrt{\frac{29}{5}}$

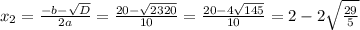
$x_2=\frac{-b-\sqrt{D}}{2a}=\frac{20-\sqrt{2320}}{10}=\frac{20-4\sqrt{145}}{10}=2-2\sqrt{\frac{29}{5}}$

Второй корень - отрицательный, нам не подходит, так как скорость отрицательной быть не может.

Поэтому скорость первого автобуса 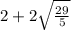$2+2\sqrt{\frac{29}{5}}$ , а скорость второго автобуса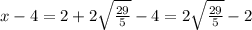 $x-4=2+2\sqrt{\frac{29}{5}}-4=2\sqrt{\frac{29}{5}}-2$

ответ: скорость первого автобуса 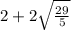$2+2\sqrt{\frac{29}{5}}$ , скорость второго автобуса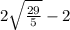 $2\sqrt{\frac{29}{5}}-2$

MOGZ ответил